Lesson 4: How Many Groups? (Part 1)

Let’s play with blocks and diagrams to think about division with fractions.

4.1: Equal-sized Groups

Write a multiplication equation and a division equation for each statement or diagram.

  1. Eight \$5 bills are worth \$40.
  2. There are 9 thirds in 3 ones.
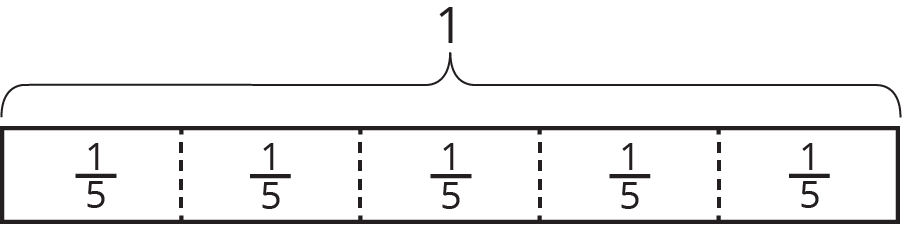
  1. A tape diagram of 5 equal parts. Each part is labeled one fifth. Above the bar is a bracket, labeled 1, that spans the entire length of the bar.

4.2: Reasoning with Pattern Blocks

Use the pattern blocks in the applet to answer the questions. (If you need help aligning the pieces, you can turn on the grid.)

GeoGebra Applet EpztQZ6y

  1. If a hexagon represents 1 whole, what fraction do each of the following shapes represent? Be prepared to show or explain your reasoning.
    1. 1 triangle
    2. 1 rhombus
    3. 1 trapezoid
    4. 4 triangles
    5. 3 rhombuses
    6. 2 hexagons
    7. 1 hexagon and 1 trapezoid

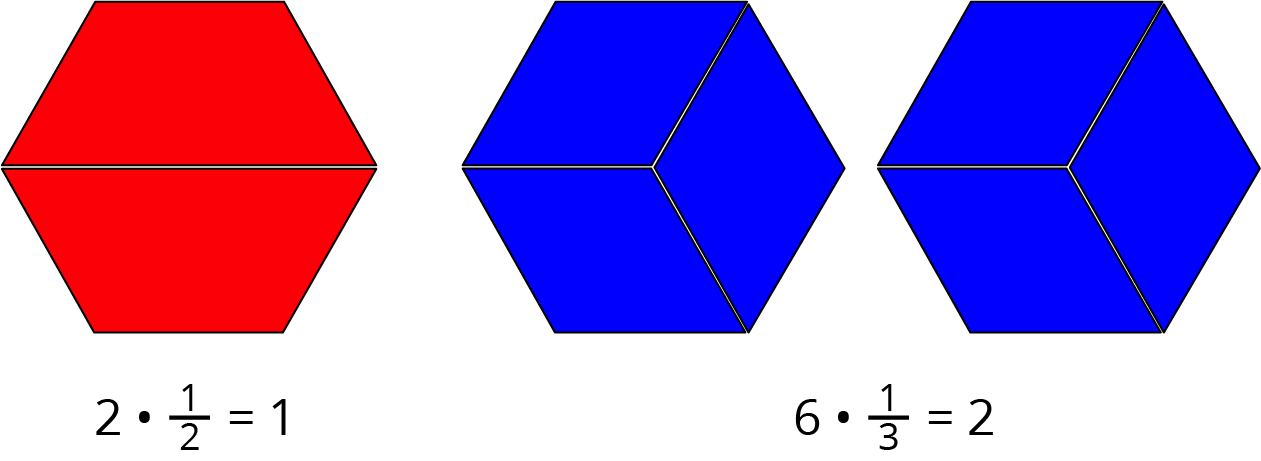
  2. Here are Elena’s diagrams for $2 \boldcdot \frac12 = 1$ and $6 \boldcdot \frac13 = 2$. Do you think these diagrams represent the equations? Explain or show your reasoning.

    “”
  3. Use pattern blocks to represent each multiplication equation. Recall that a hexagon represents 1 whole.

    1. $3 \boldcdot \frac 16=\frac12$

    2. $2 \boldcdot \frac 32=3$
  4. Answer the following questions. If you get stuck, use pattern blocks.

    1. How many $\frac 12$s are in 4?

    2. How many $\frac23$s are in 2?

    3. How many $\frac16$s are in $1\frac12$?

Summary

Some problems that involve equal-sized groups also involve fractions. Here is an example: “How many $\frac16$ are in 2?” We can express this question with multiplication and division equations. $${?} \boldcdot \frac16 = 2$$ $$2 \div \frac16 = {?}$$

Pattern-block diagrams can help us make sense of such problems. Here is a set of pattern blocks.

Four pattern blocks: One large yellow hexagon, one blue rhombus, one red trapezoid, and one green triangle.

If the hexagon represents 1 whole, then a triangle must represent $\frac16$, because 6 triangles make 1 hexagon. We can use the triangle to represent the $\frac 16$ in the problem.

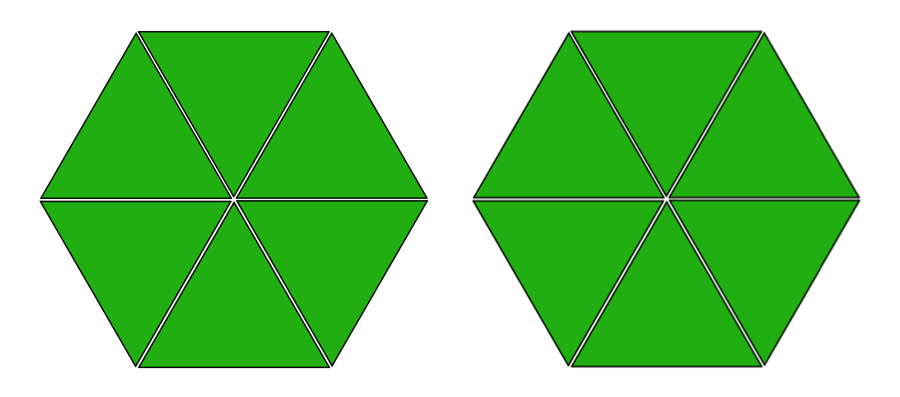
Twelve triangles make 2 hexagons, which means there are 12 groups of $\frac16$ in 2.

If we write the 12 in the place of the “?” in the original equations, we have: $$12 \boldcdot \frac16 = 2$$

$$2 \div \frac16 = 12$$

Practice Problems ▶