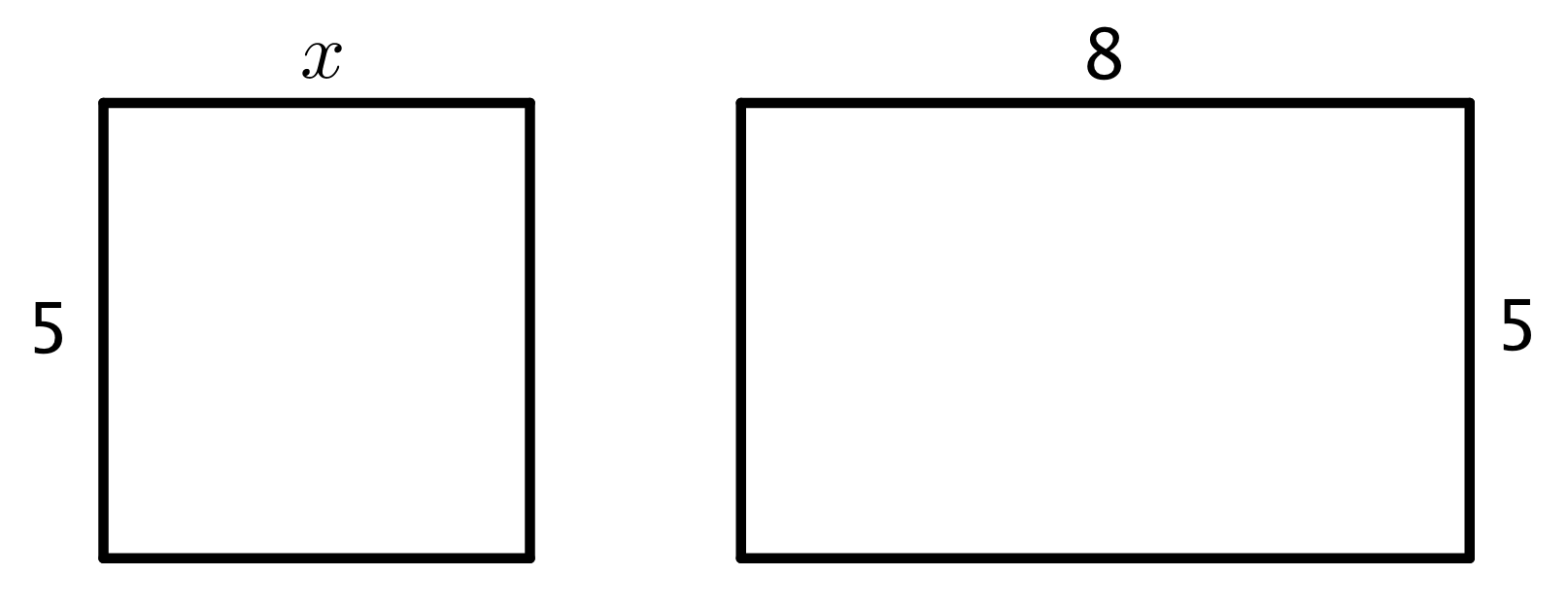
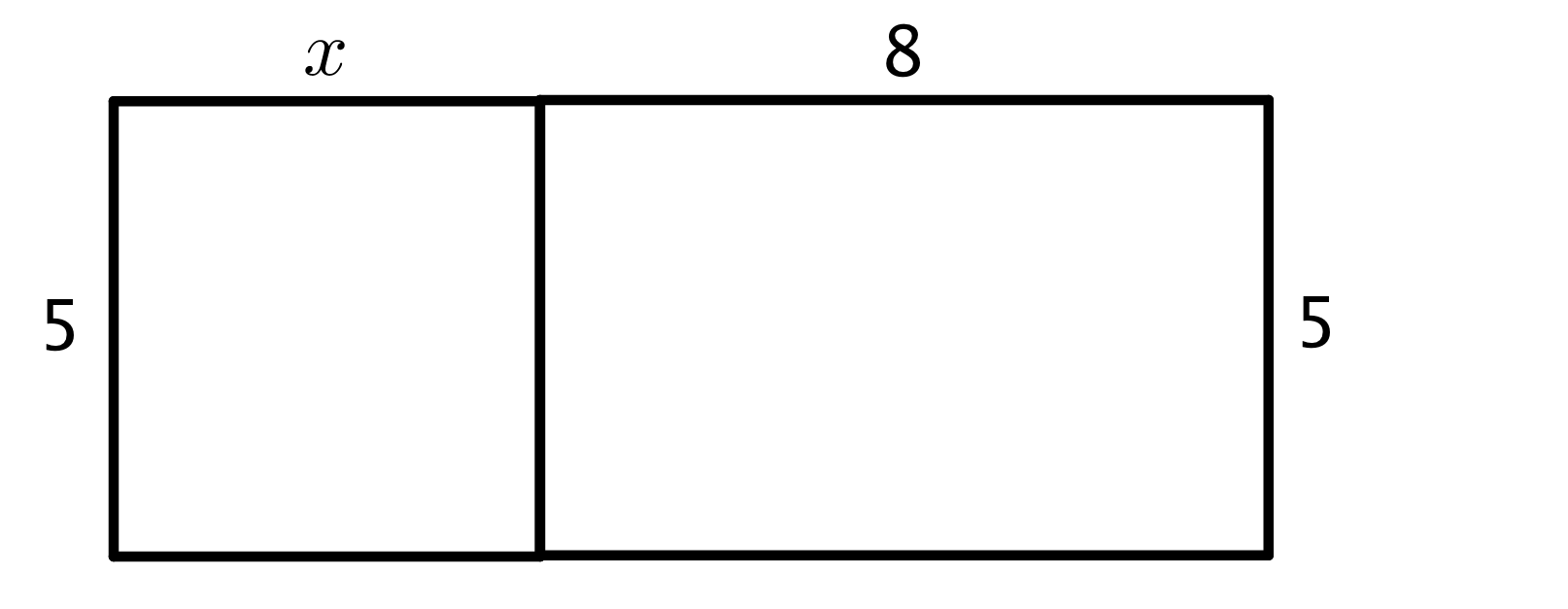
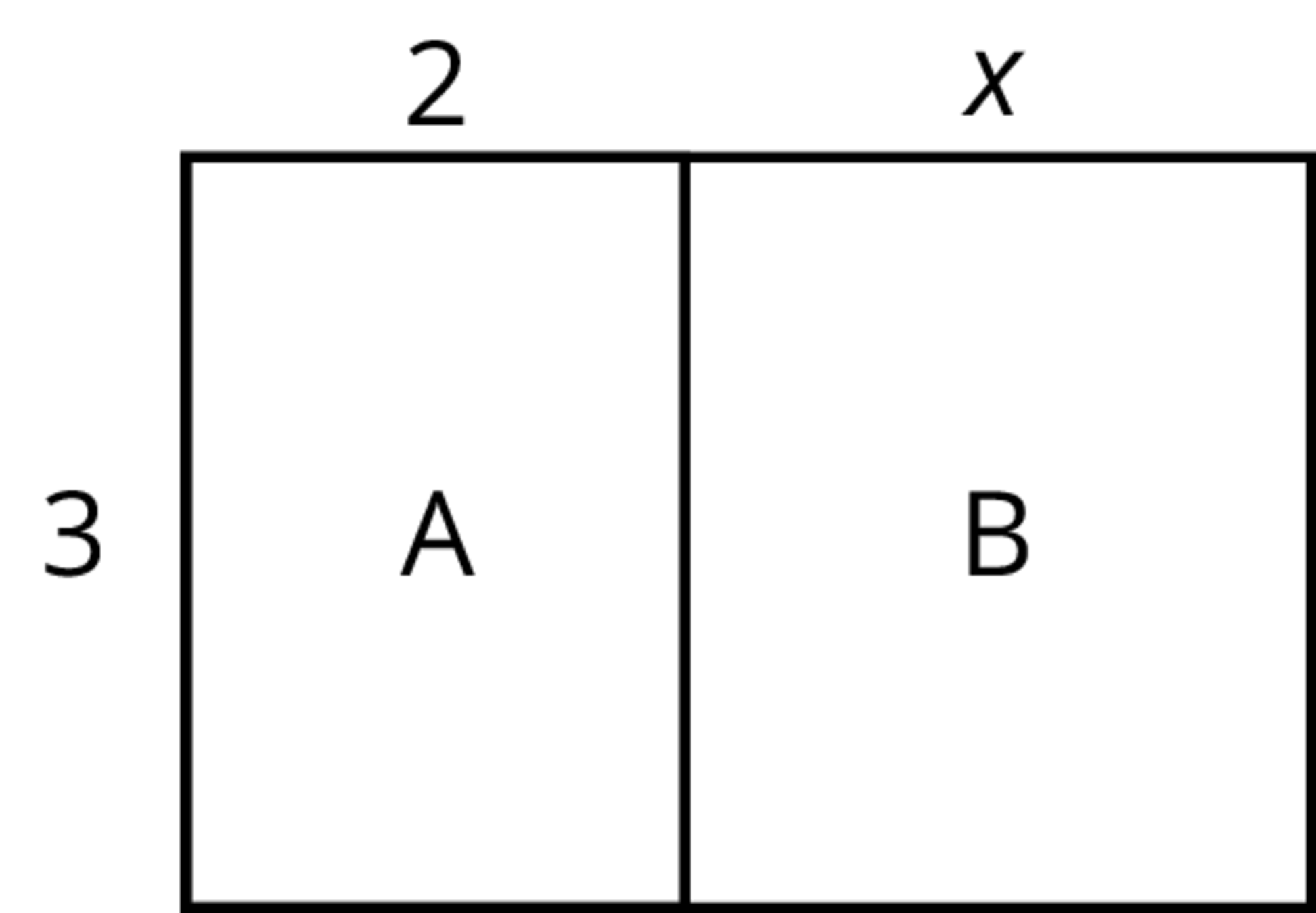
Here is a rectangle composed of two smaller rectangles A and B.
Based on the drawing, we can make several observations about the area of the rectangle:
- One side length of the large rectangle is 3 and the other is $2+x$, so its area is $3(2+x)$.
- Since the large rectangle can be decomposed into two smaller rectangles, A and B, with no overlap, the area of the large rectangle is also the sum of the areas of rectangles A and B: $3(2) + 3(x)$ or $6+3x$.
- Since both expressions represent the area of the large rectangle, they are equivalent to each other. $3(2+x)$ is equivalent to $6 + 3x$.
We can see that multiplying 3 by the sum $2+x$ is equivalent to multiplying 3 by 2 and then 3 by $x$ and adding the two products. This relationship is an example of the distributive property.
$$3(2+x) = 3 \boldcdot 2 + 3 \boldcdot x$$