Lesson 9: How Much in Each Group? (Part 2)

Let’s practice dividing fractions in different situations.

9.1: Number Talk: Greater Than 1 or Less Than 1?

Decide whether each of the following is greater than 1 or less than 1.

  1. \frac12\div\frac14
  2. 1\div\frac34
  3. \frac23\div\frac78
  4. 2\frac78\div2\frac35

9.2: Two Water Containers

  1. After looking at these pictures, Lin says, “I see the fraction \frac 25.” Jada says, “I see the fraction \frac 34.” What quantities are Lin and Jada referring to?

  2. How many liters of water fit in the water dispenser?

    Write a multiplication equation and a division equation for the question, then find the answer. Draw a diagram, if needed. Check your answer using the multiplication equation.

9.3: Amount in One Group

Write a multiplication equation and a division equation and draw a diagram to represent each situation and question. Then find the answer. Explain your reasoning.

  1. Jada bought 3\frac12 yards of fabric for $21. How much did each yard cost?
  2. \frac 49 kilogram of baking soda costs $2. How much does 1 kilogram of baking soda cost?
  3. Diego can fill 1\frac15 bottles with 3 liters of water. How many liters of water fill 1 bottle?
  4. \frac54 gallons of water fill \frac56 of a bucket. How many gallons of water fill the entire bucket?

9.4: Inventing a Situation

  1. Think of a situation that involves a question that can be represented by \frac{1}{3}\div\frac14 = {?} Write a description of that situation and the question.

  2. Trade descriptions with a member of your group.

    • Review each other’s description and discuss whether each invented question is an appropriate match for the equation.
    • Revise your description or question based on feedback from your partner.
  3. Find the answer to your question. Explain or show your reasoning. If you get stuck, draw a diagram.

Summary

Sometimes we have to think carefully about how to solve a problem that involves multiplication and division. Diagrams and equations can help us. 

Let’s take this example: \frac34 of a pound of rice fills \frac25 of a container. 

There are two whole amounts to keep track of: 1 whole pound, and 1 whole container. The equations we write and the diagram we draw depend on what question we are trying to answer. Here are two questions that could be asked:

  • How many pounds fill 1 container?
  • What fraction of a container does 1 pound fill?

We can represent and answer the first question (how many pounds fill a whole container) with:

\frac 25 \boldcdot {?} = \frac 34

\frac 34 \div \frac 25 = {?}

 

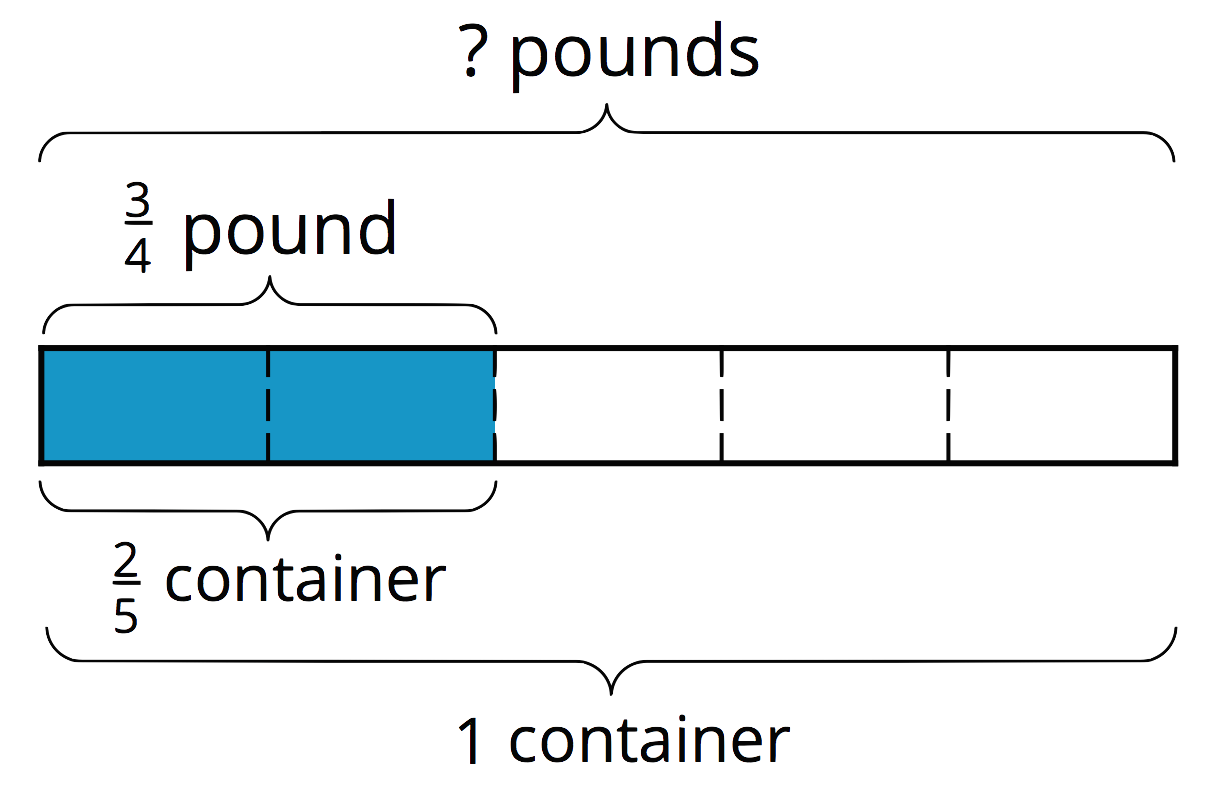
If \frac25 of a container is filled with \frac 34 pound, then \frac 15 of a container is filled with half of \frac34, or \frac38, pound. One whole container then has 5 \boldcdot \frac38 (or \frac {15}{8}) pounds.

We can represent and answer the second question (what fraction of the container 1 pound fills) with:

\frac34 \boldcdot {?} = \frac25

\frac25 \div \frac34 ={?}

 

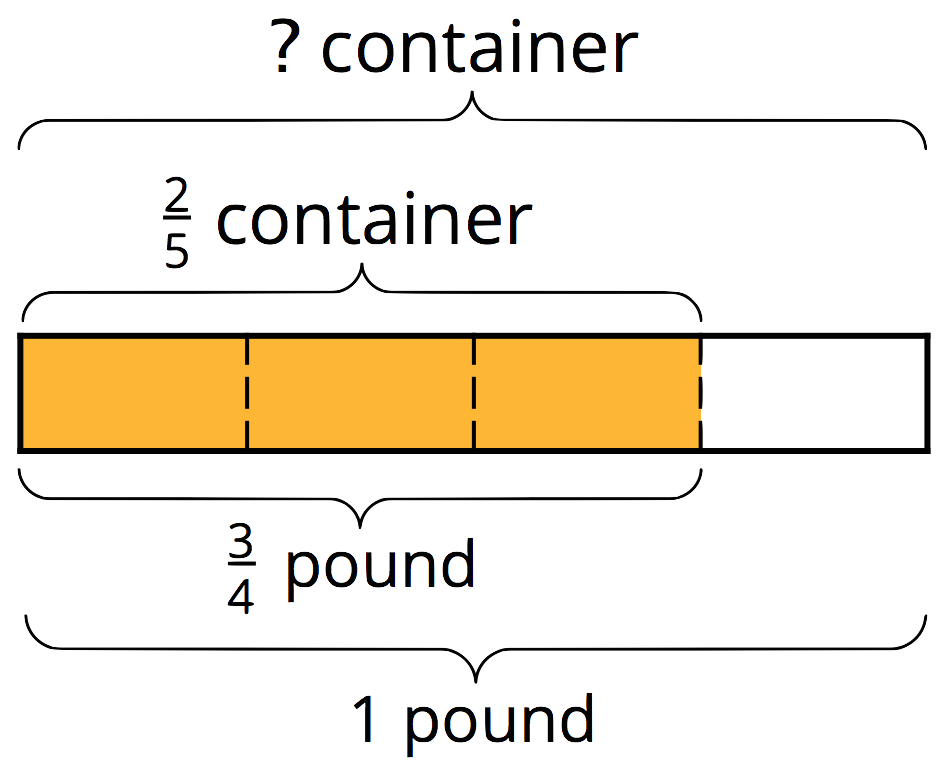
If \frac 34 pound fills \frac25 of a container, then \frac14 pound fills a third of \frac25, or \frac {2}{15}, of a container. One whole pound then fills 4 \boldcdot \frac{2}{15} (or \frac {8}{15}) of a container.

Practice Problems ▶