Lesson 13: Interpreting Points on a Coordinate Plane

Let’s examine what points on the coordinate plane can tell us.

13.1: Unlabeled Points

Label each point on the coordinate plane with the appropriate letter and ordered pair.

$A = (7, \text-5.5)$

$B = (\text-8, 4)$

$C = (3, 2)$

$D = (\text-3.5, 0.2)$

 

13.2: Account Balance

The graph shows the balance in a bank account over a period of 14 days. The axis labeled $b$ represents account balance in dollars. The axis labeled $d$ represents the day.

  1. Estimate the greatest account balance. On which day did it occur?
  2. Estimate the least account balance. On which day did it occur?
  3. What does the point $(6, \text-50)$ tell you about the account balance?
  4. How can we interpret $| \text- 50|$ in the context?

13.3: High and Low Temperatures

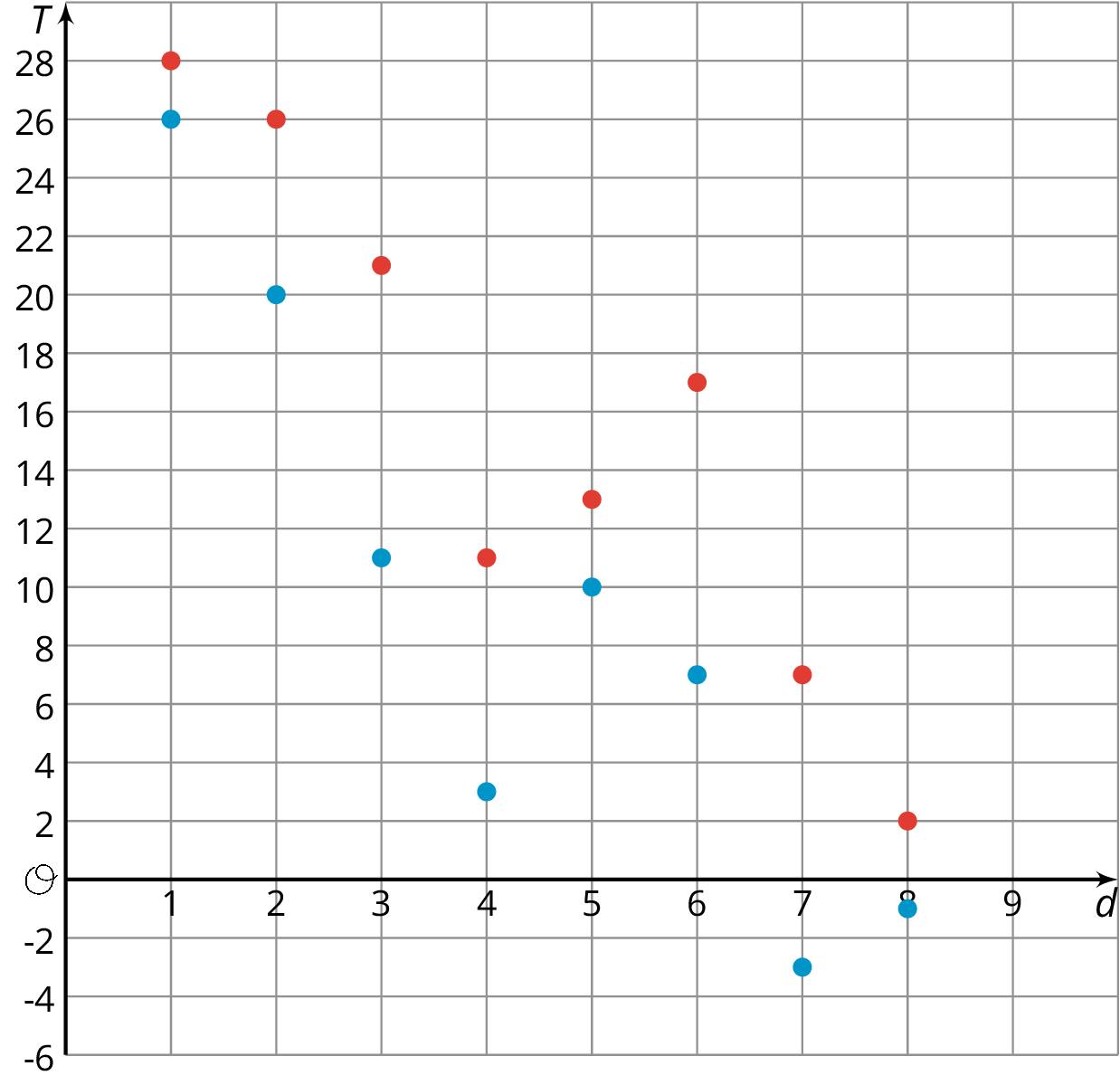
The coordinate plane shows the high and low temperatures in Nome, Alaska over a period of 8 days. The axis labeled $T$ represents temperatures in degrees Fahrenheit. The axis labeled $d$ represents the day.

A graph of 16 points plotted on a coordinate plane with the origin labeled "O". The numbers 1 through 9 are indicated on the the d axis. The numbers negative 6 through 28, in increments of 2, are indicated on the T axis. The data points are presented in the following 8 groups. Group 1. 1 comma 28 and 1 comma 26. Group 2. 2 comma 26 and 2 comma 20. Group 3. 3 comma 21 nad 3 comma 11. Group 4. 4 comma 11 and 4 comma 3. Group 5. 5 comma 13 and 5 comma 10. Group 6. 6 comma 17 and 7 comma 7. Group 7. 7 comma 7 and 7 comma negative 3. Group 8. 8 comma 2 and 8 comma negative 1.
    1. What was the warmest high temperature?
    2. Write an inequality to describe the high temperatures, $H$, over the 8-day period.
    1. What was the coldest low temperature?
    2. Write an inequality to describe the low temperatures, $L$, over the 8-day period.
    1. On which day(s) did the largest difference between the high and low temperatures occur? Write down this difference.
    2. On which day(s) did the smallest difference between the high and low temperatures occur? Write down this difference.

Summary

Points on the coordinate plane can give us information about a context or a situation. One of those contexts is about money.

To open a bank account, we have to put money into the account. The account balance is the amount of money in the account at any given time. If we put in \$350 when opening the account, then the account balance will be 350.

Sometimes we may have no money in the account and need to borrow money from the bank. In that situation, the account balance would have a negative value. If we borrow \$200, then the account balance is -200.

A coordinate grid can be used to display both the balance and the day or time for any balance. This allows to see how the balance changes over time or to compare the balances of different days.

Similarly, if we plot on the coordinate plane data such as temperature over time, we can see how temperature changes over time or compare temperatures of different times.

Practice Problems ▶