15.1: Notice and Wonder: Wrapping Paper
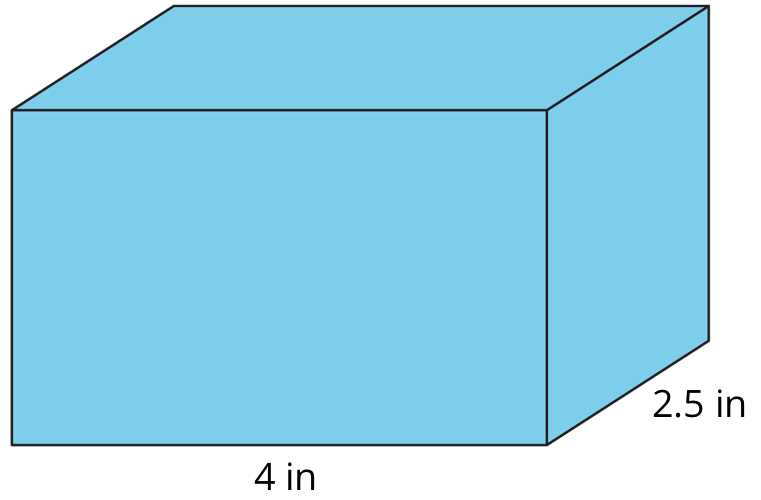
Kiran is wrapping this box of sports cards as a present for a friend.
What do you notice? What do you wonder?
Lesson 15: More Nets, More Surface Area
Let’s draw nets and find the surface area of polyhedra.
15.2: Building Prisms and Pyramids
Your teacher will give you a drawing of a polyhedron. You will draw its net and calculate its surface area.
-
What polyhedron do you have?
-
Study your polyhedron. Then, draw its net on graph paper. Use the side length of a grid square as the unit.
-
Label each polygon on the net with a name or number.
-
Find the surface area of your polyhedron. Show your thinking in an organized manner so that it can be followed by others.
When finished, pause for additional instructions from your teacher.
15.3: Comparing Boxes
Here are the nets of three cardboard boxes that are all rectangular prisms. The boxes will be packed with 1-centimeter cubes. All lengths are in centimeters.
- Compare the surface areas of the boxes. Which box will use the least cardboard? Show your reasoning.
- Now compare the volumes of these boxes in cubic centimeters. Which box will hold the most 1-centimeter cubes? Show your reasoning.
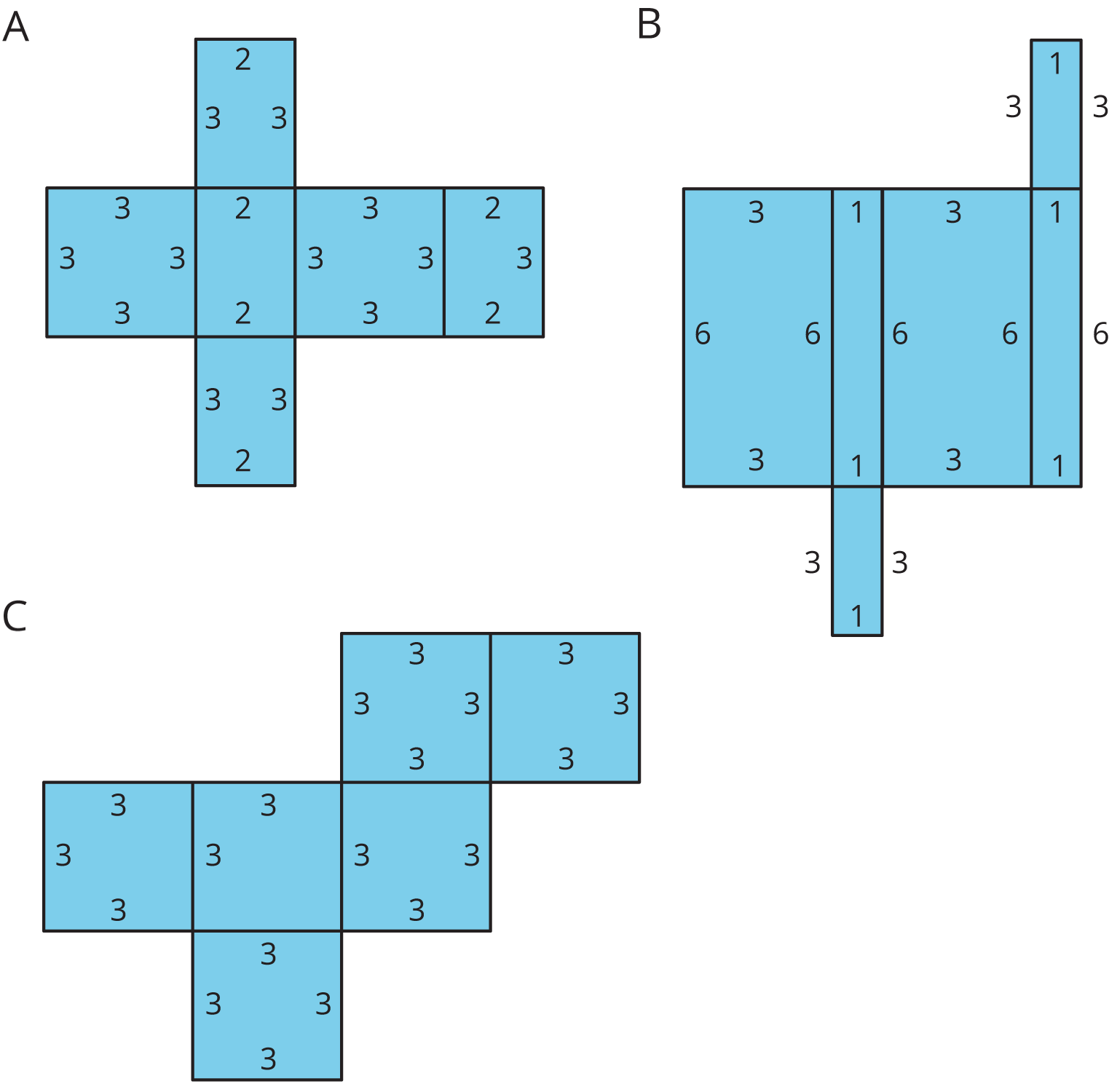
Figure C shows a net of a cube. Draw a different net of a cube. Draw another one. And then another one. How many different nets can be drawn and assembled into a cube?
Summary
The surface area of a polyhedron is the sum of the areas of all of the faces.
Because a net shows us all faces of a polyhedron at once, it can help us find the surface area. We can find the areas of all polygons in the net and add them.
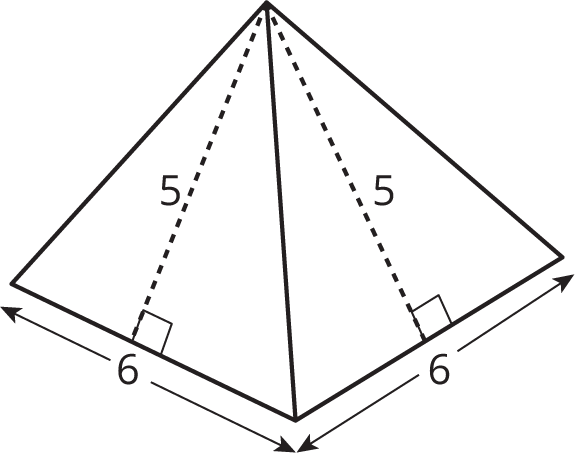
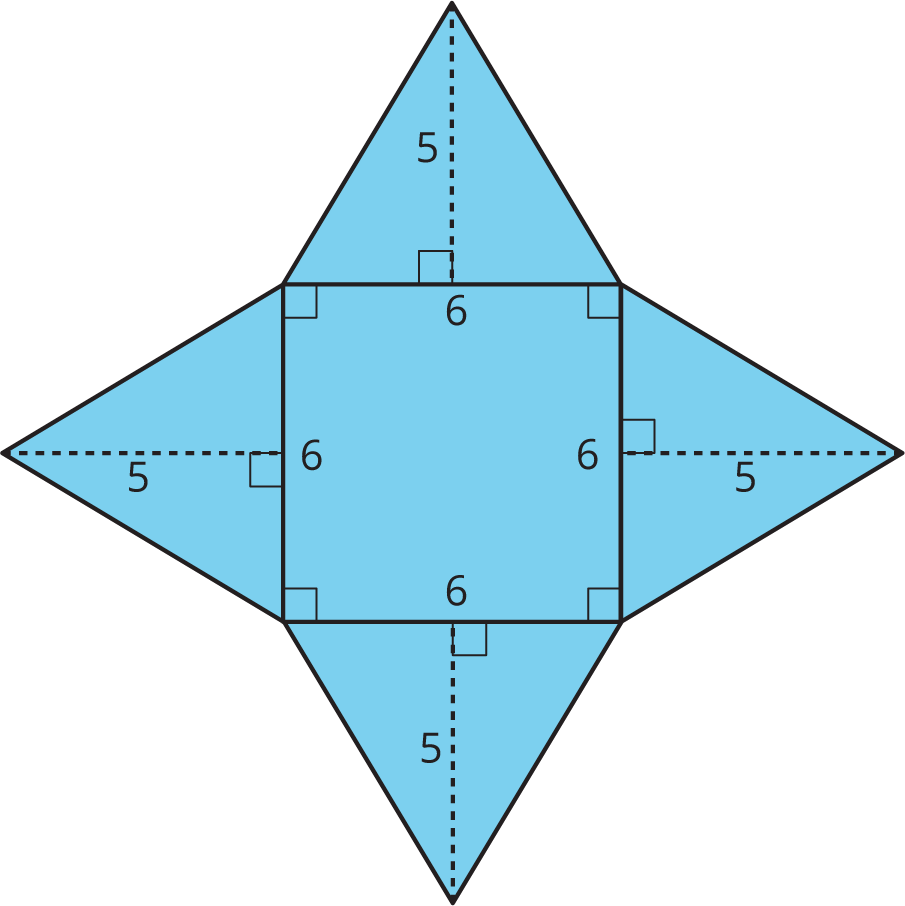
A square pyramid has a square and four triangles for its faces. Its surface area is the sum of the areas of the square base and the four triangular faces: $$(6\boldcdot 6) + 4\boldcdot \left(\frac12 \boldcdot 5 \boldcdot 6\right) = 96$$ The surface area of this square pyramid is 96 square units.