Lesson 13: Rectangles with Fractional Side Lengths

Let’s explore rectangles that have fractional measurements.

13.1: Areas of Squares

Three squares. The first square is labeled with side length 1 inch on the vertical side and 1 inch on the horizontal side. The second square is labeled with side length one half inch on the vertical side and one half inch on the horizontal side. The third square is labeled with side length 2 inches on the vertical side and 2 inches on the horizontal side.
  1. What do you notice about the areas of the squares? Write your observations.
  2. Consider the statement: “A square with side lengths of \frac13 inch has an area of \frac13 square inches.” Do you agree or disagree with the statement? Explain or show your reasoning.

13.2: Areas of Squares and Rectangles

Use one piece of \frac14-inch graph paper for the following.

  1. Use a ruler to draw a square with side length of 1 inch on the graph paper. Inside the square, draw a square with side length of \frac14 inch.

    1. How many squares with side length of \frac 14 inch can fit in a square with side length of 1 inch?
    2. What is the area of a square with side length of \frac 14 inch? Explain or show how you know.

  2. Use a ruler to draw a rectangle that is 3\frac12 inches by 2\frac14 inches on the graph paper. Write a division expression for each question and answer the question.

    1. How many \frac14-inch segments are in a length of 3\frac12 inches? 
    2. How many \frac14-inch segments are in a length of 2\frac14 inches? 
  3. Use your drawings to show that a rectangle that is 3\frac12 inches by 2\frac14 inches has an area of 7\frac 78 square inches.

13.3: Areas of Rectangles

Each of the following multiplication expressions represents the area of a rectangle.

2 \boldcdot 4

2\frac12 \boldcdot 4

2 \boldcdot 4\frac 34

2\frac12 \boldcdot 4\frac34

  1. All regions shaded in light blue have the same area. Match each diagram to the expression that you think represents its area. Be prepared to explain your reasoning.

  2. Use the diagram that matches 2\frac12 \boldcdot 4\frac34 to show that the value of 2\frac12 \boldcdot 4\frac34 is 11\frac78.

13.4: How Many Would it Take? (Part 2)

Noah would like to cover a rectangular tray with rectangular tiles. The tray has a width of 11\frac14 inches and an area of 50\frac58 square inches.

  1. Find the length of the tray in inches.
  2. If the tiles are \frac{3}{4} inch by \frac{9}{16} inch, how many would Noah need to cover the tray completely, without gaps or overlaps? Explain or show your reasoning.
  3. Draw a diagram to show how Noah could lay the tiles. Your diagram should show how many tiles would be needed to cover the length and width of the tray, but does not need to show every tile.

Summary

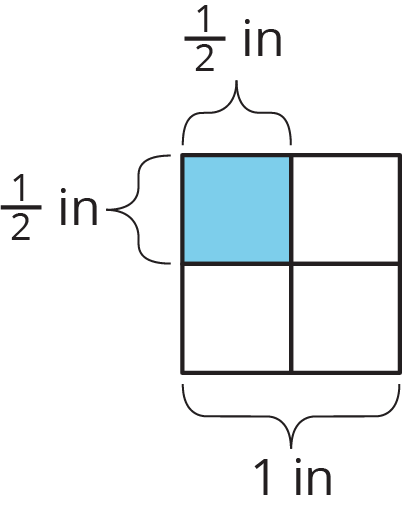
If a rectangle has side lengths a units and b units, the area is a \boldcdot b square units. For example, if we have a rectangle with \frac12-inch side lengths, its area is \frac12 \boldcdot \frac12 or \frac14 square inches.

A large square is divided into 4 equal squares. The large square has bottom horizontal side length labeled 1 inch. Of the four smaller squares, the top left square is shaded blue. It has side lengths labeled one half inch.

This means that if we know the area and one side length of a rectangle, we can divide to find the other side length.

A rectangle with the horizontal side labeled 10 and one half inches and the vertical side labeled with a question mark. In the center of the rectangle, 89 and one fourth square inches is indicated.
 

If one side length of a rectangle is 10\frac12 in and its area is 89\frac14 in2, we can write this equation to show their relationship: \frac12  \boldcdot {?} =89\frac14

Then, we can find the other side length, in inches, using division: 89\frac14 \div 10\frac12 = {?}

Practice Problems ▶