Unit 1: Practice Problem Sets

Lesson 1

Problem 1

Which square—large, medium, or small—covers more of the plane? Explain your reasoning.

A plane composed of a series of squares. There are 5 large squares, 10 medium squares, and 10 small squares.

 

Problem 2

Draw three different quadrilaterals, each with an area of 12 square units.

Problem 3

Use copies of the rectangle to show how a rectangle could:

a. tile the plane.

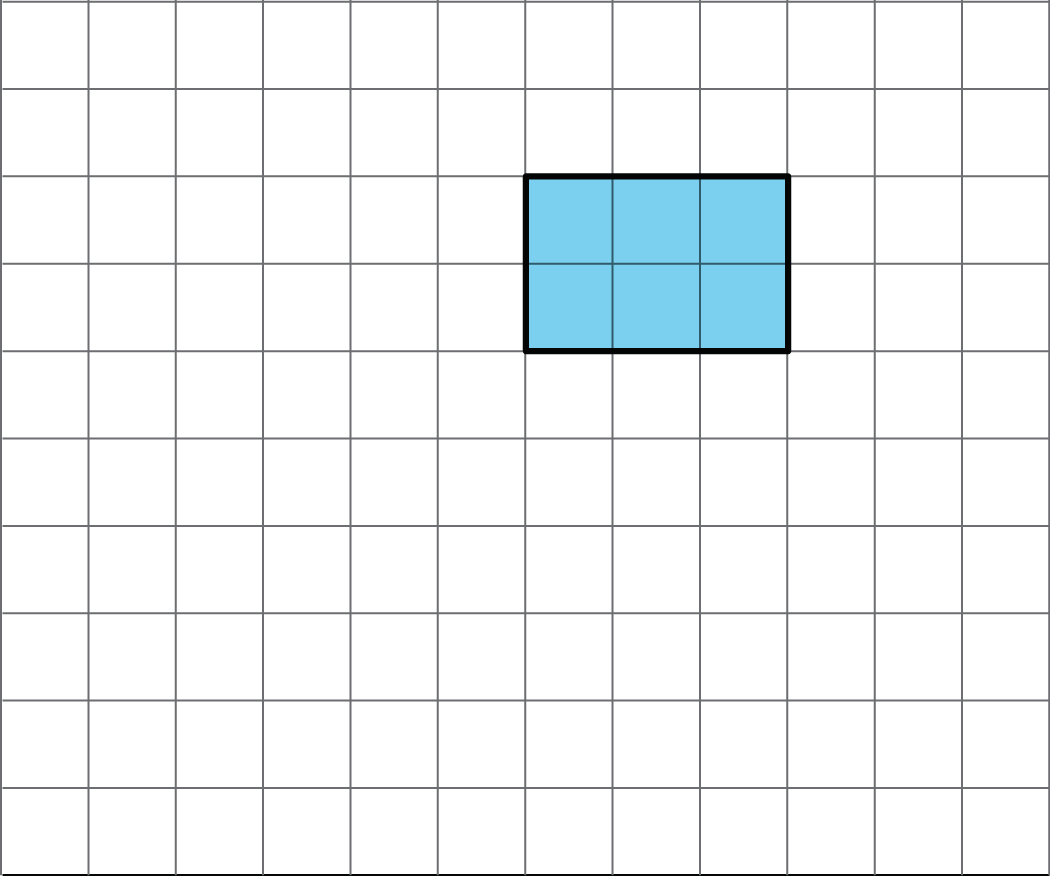
b. not tile the plane.

Problem 4

The area of this shape is 24 square units. Which of these statements is true about the area? Select all that apply.

A figure with a top side of 4 units and a bottom side of 6 units. The lower portion of the figure has sides that are 2 units tall, and the upper portion has sides that 3 units tall. All angles are right angles.

  1. The area can be found by counting the number of squares that touch the edge of the shape.

  2. It takes 24 grid squares to cover the shape without gaps and overlaps.

  3. The area can be found by multiplying the sides lengths that are 6 units and 4 units.

  4. The area can be found by counting the grid squares inside the shape.
  5. The area can be found by adding $4 \times 3$ and $6 \times 2$.

Problem 5

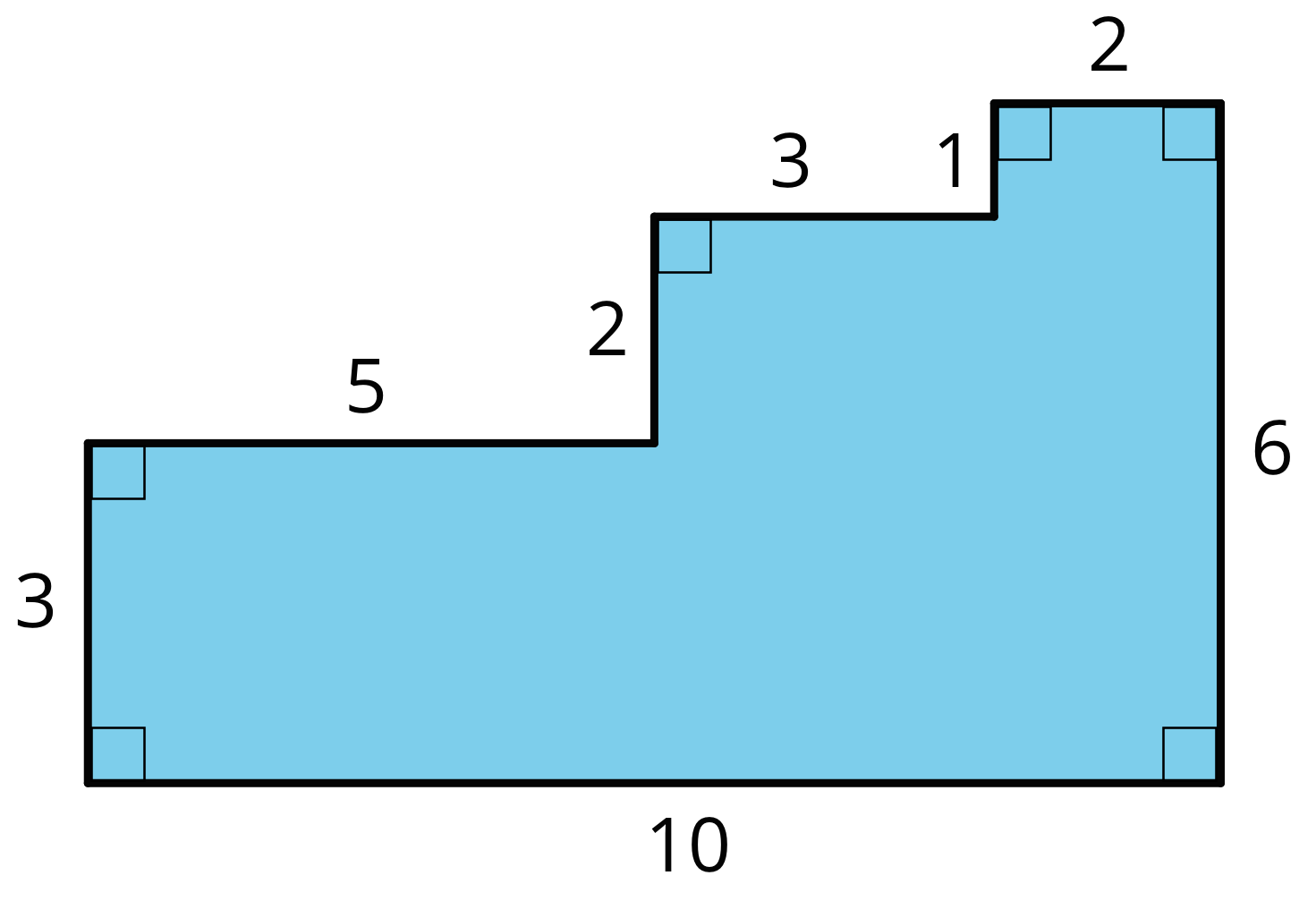
Here are two copies of the same figure. Show two different ways for finding the area of the shaded region. All angles are right angles.

A figure with a bottom of 10 units, a right side of six units, and a left side that rises 3 units, then goes across 5 units, then goes up another 2 units, then across another 3 units, then up another 1 unit, and across another 2 units to connect to the right side. All angles are right angles.

A figure with a bottom of 10 units, a right side of six units, and a left side that rises 3 units, then goes across 5 units, then goes up another 2 units, then across another 3 units, then up another 1 unit, and across another 2 units to connect to the right side. All angles are right angles.

Problem 6

Which shape has a larger area: a rectangle that is 7 inches by $\frac 34$ inch, or a square with side length of $2 \frac12$ inches? Show your reasoning.

Lesson 2

Problem 1

The diagonal of a rectangle is shown.

  1. Decompose the rectangle along the diagonal, and recompose the two pieces to make a different shape.

  2. How does the area of this new shape compare to the area of the original rectangle? Explain how you know.

Problem 2

 

The area of the square is 1 square unit. Two small triangles can be put together to make a square or to make a medium triangle.

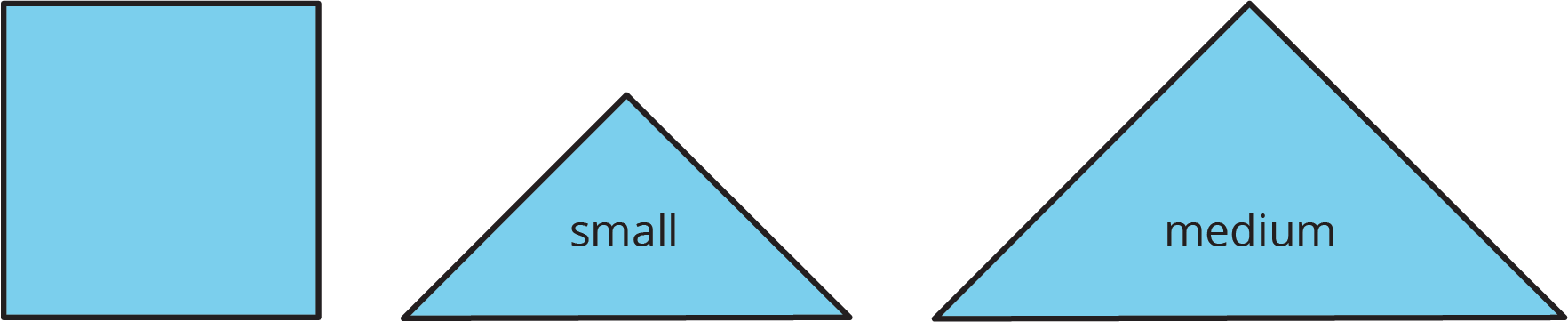
Three figures. A square, a small triangle, and a medium triangle.

Which figure also has an area of $1\frac 12$ square units? Select all that apply.

Four figures labeled A, B, C, and D. Figure A is composed of three small triangles, figure B is composed of three small triangles in a different arrangement, figure C is composed of one medium triangle and one small triangle, and figure D is composed of two small triangles and one square.

Problem 3

Priya decomposed a square into 16 smaller, equal-size squares and then cut out 4 of the small squares and attached them around the outside of original square to make a new figure.

How does the area of her new figure compare with that of the original square?

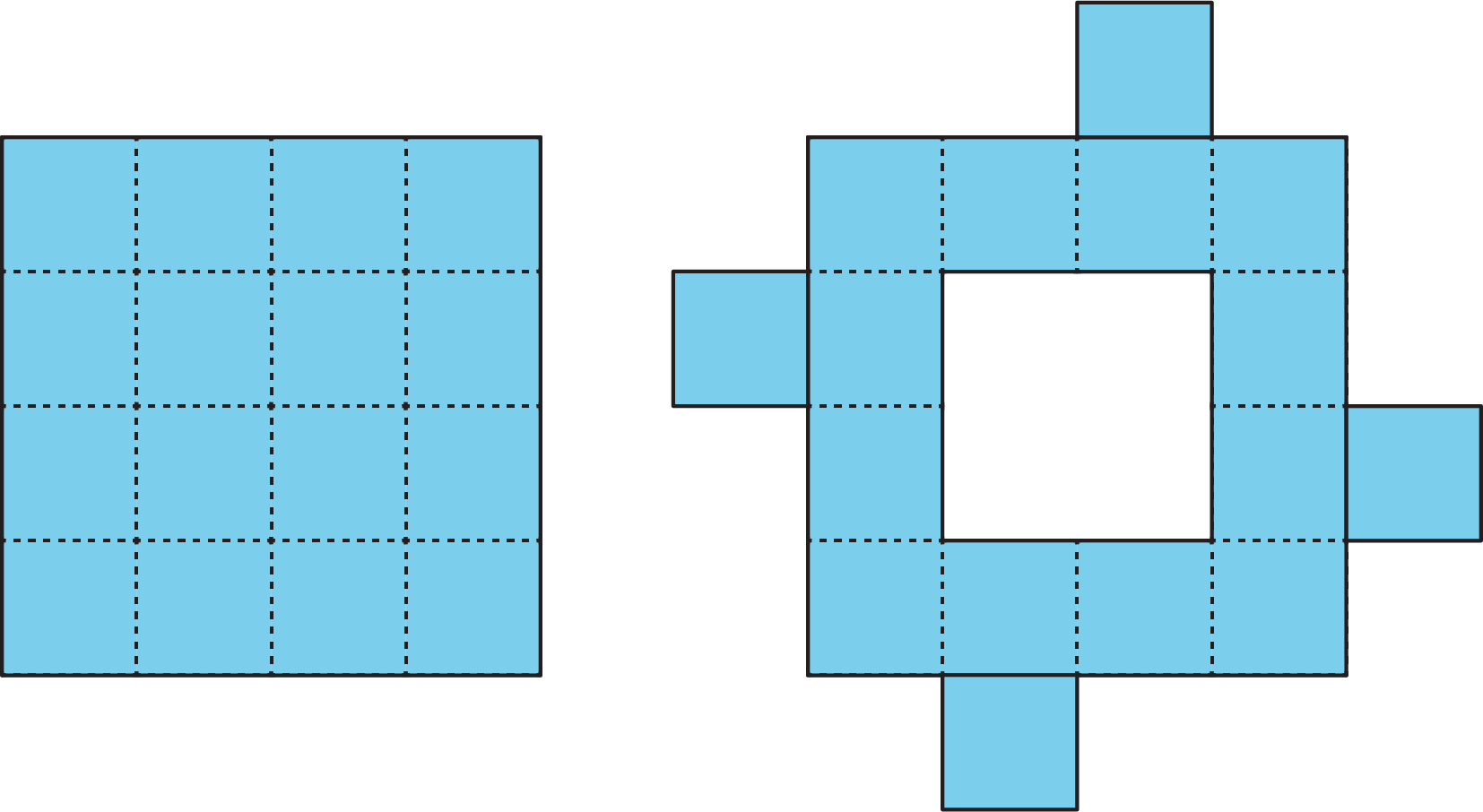
Two shapes. The first is a square comprised of 16 small squares arranged in four rows of 4. The second image has the center four squares removed and a square added to the outside of each side of the square.

  1. The area of the new figure is greater.
  2. The two figures have the same area.
  3. The area of the original square is greater.
  4. We don’t know because neither the side length nor the area of the original square is known.

Problem 4 (from Unit 1, Lesson 1)

The area of a rectangular playground is 78 square meters. If the length of the playground is 13 meters, what is its width?

Problem 5 (from Unit 1, Lesson 1)

A student said, “We can’t find the area of the shaded region because the shape has many different measurements, instead of just a length and a width that we could multiply.”

A multi-sided figure. The sides on top measure 10 units, 35 units, and 15 units. Two of the three sides on the left measure 10 units. One of the two sides on the right measures 10 units. One of the two sides on the bottom measure 15 units. The total width of the figure is 60 units, and the total height is 30 units. All angles are right angles.

 

Explain why the student’s statement about area is incorrect.

Lesson 3

Problem 1

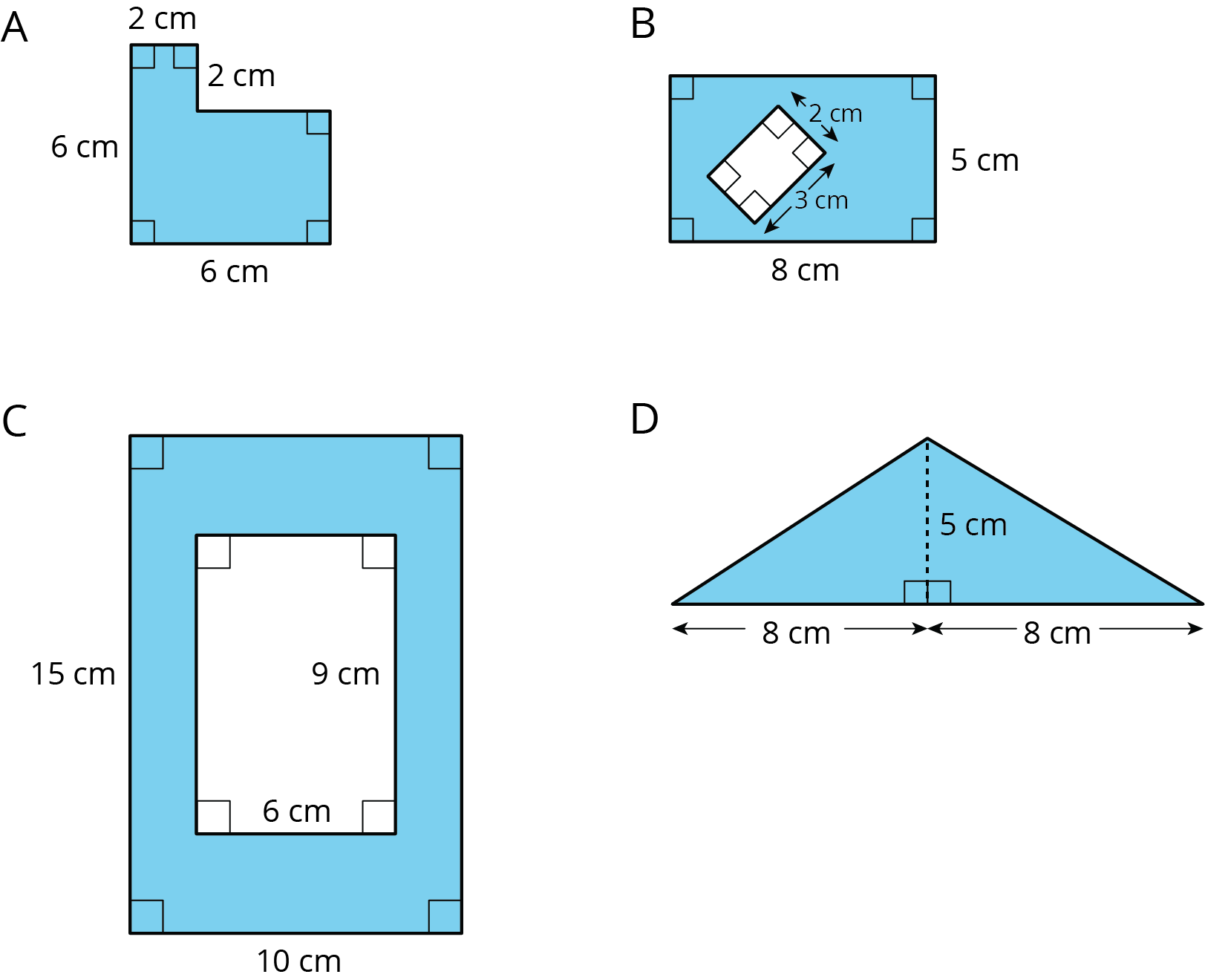
Find the area of each shaded region. Show your reasoning.

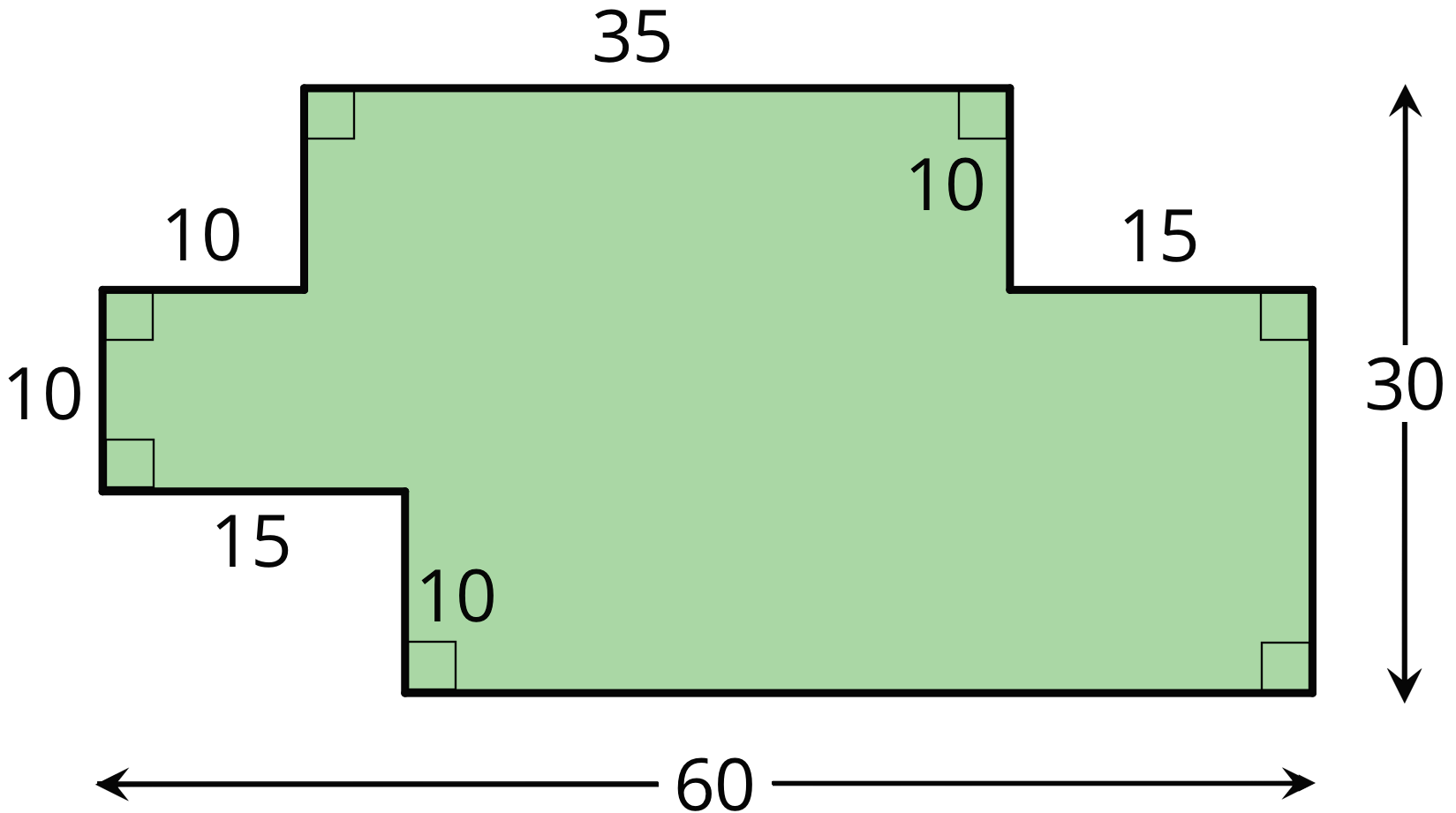
Problem 2

Find the area of each shaded region. Show or explain your reasoning.

Problem 3

Two plots of land have very different shapes. Noah said that both plots of land have the same area.

Two shapes labeled “plot A” and “plot B”. Plot “A“is a rectangle and plot “B” is the same height, but has a triangular shape removed from the right side, and an identical triangle shape added to the left side.

Do you agree with Noah? Explain your reasoning.

Problem 4 (from Unit 1, Lesson 2)

A homeowner is deciding on the size of tiles to use to fully tile a rectangular wall in her bathroom that is 80 inches by 40 inches. The tiles are squares and come in three side lengths: 8 inches, 4 inches, and 2 inches. State if you agree with each statement about the tiles. Explain your reasoning.

  1. Regardless of the size she chooses, she will need the same number of tiles.
  2. Regardless of the size she chooses, the area of the wall that is being tiled is the same.
  3. She will need two 2-inch tiles to cover the same area as one 4-inch tile.
  4. She will need four 4-inch tiles to cover the same area as one 8-inch tile.
  5. If she chooses the 8-inch tiles, she will need a quarter as many tiles as she would with 2-inch tiles.

Lesson 4

Problem 1

Select all of the parallelograms. For each figure that is not selected, explain how you know it is not a parallelogram. 

Problem 2

a. Decompose and rearrange this parallelogram to make a rectangle.

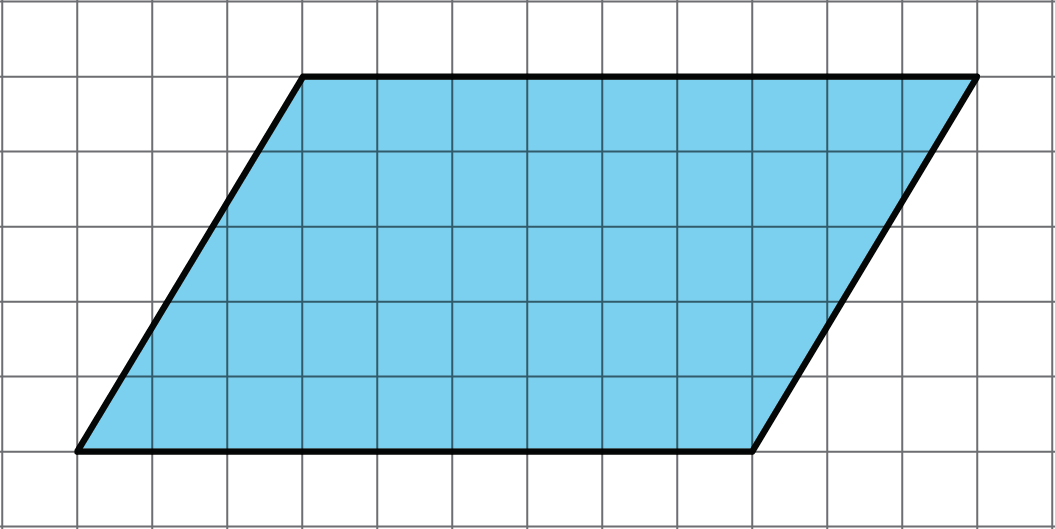
b. What is the area of the parallelogram? Explain your reasoning.

Problem 3

Find the area of the parallelogram.

A parallelogram with one side labeled 3.2 centimeters, and another side labeled 10 centimeters. A dashed line perpendicular to the 10 centimeter sides is labeled 3 centimeters

Problem 4

Explain why this quadrilateral is not a parallelogram.

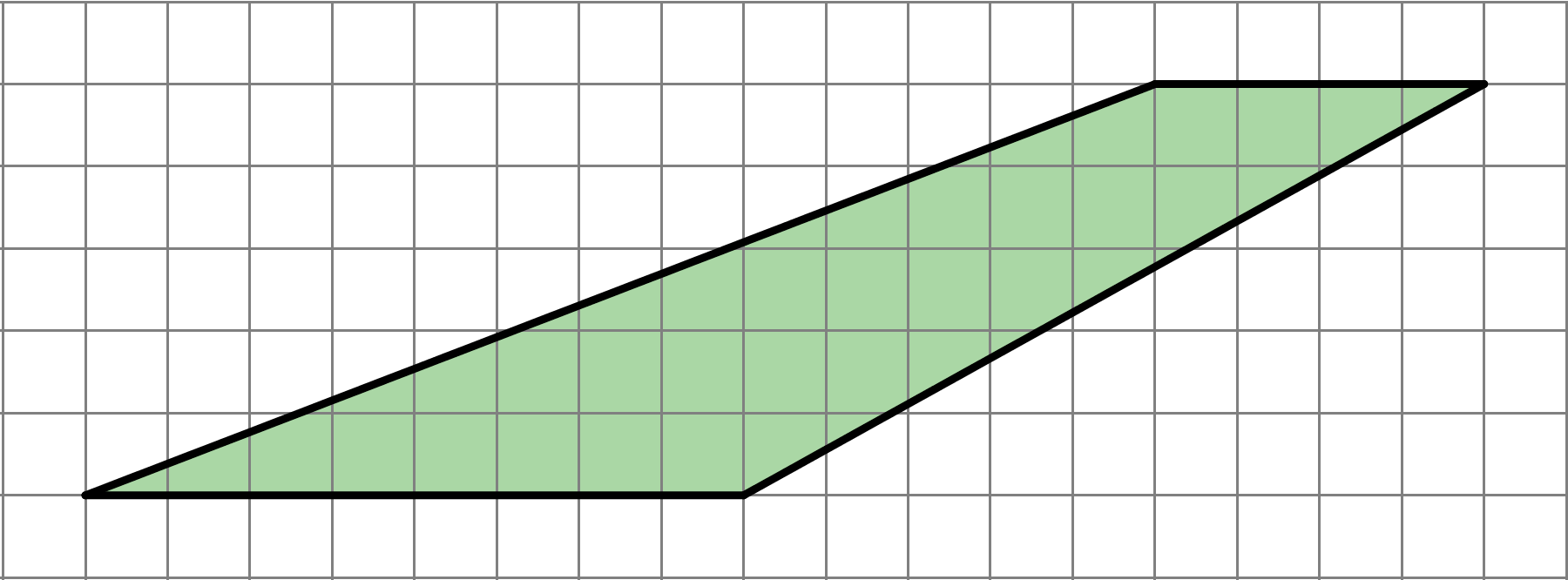
A quadrilateral with a bottom side length of 8 units, a top side length of 4 units. The left side ascends 5 units while moving right 13 units, and the right side ascends 5 units while moving right 9 units.

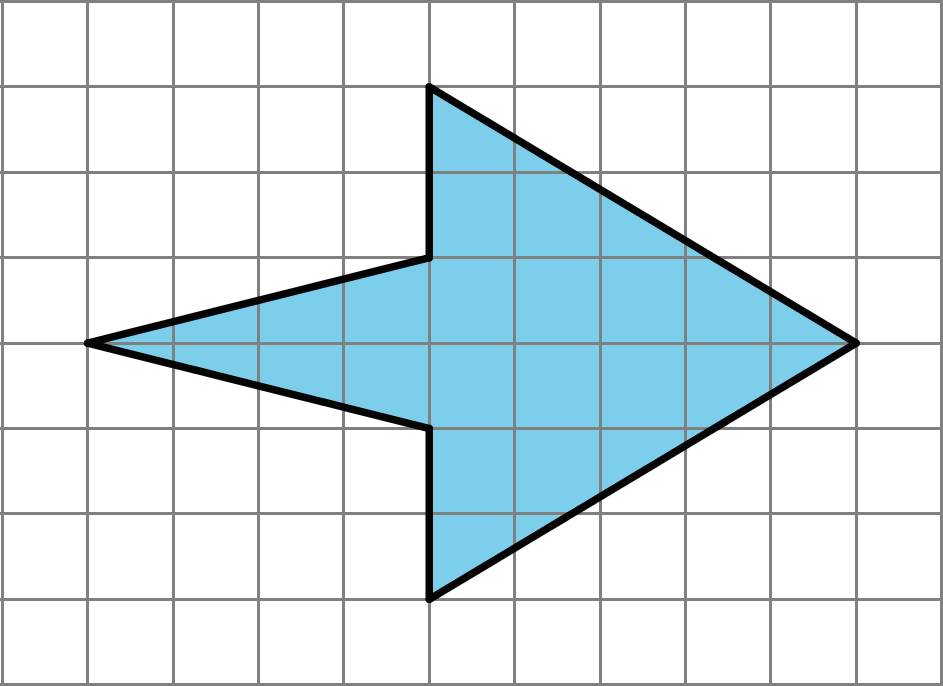
Problem 5 (from Unit 1, Lesson 3)

Find the area of each shape. Show your reasoning.

A shape with eight sides. Four sides are straight sides and extend left, right, up and, down for 2 units each. The remaining sides are angled sides connecting each of the straight sides to the next. The shape is a total of 6 units tall and 6 units wide.
A shape with six sides. It is 9 units long and six units wide at it’s widest point. Two vertical sides connect four sloped sides, which meet at either end of the shape.

Problem 6 (from Unit 1, Lesson 1)

Find the areas of the rectangles with the following side lengths.

  1. 5 in and $\frac13$ in

  2. 5 in and $\frac 43$ in

  1. $\frac 52$ in and $\frac 43$ in

  2. $\frac 7 6$ in and $\frac 67$ in

Lesson 5

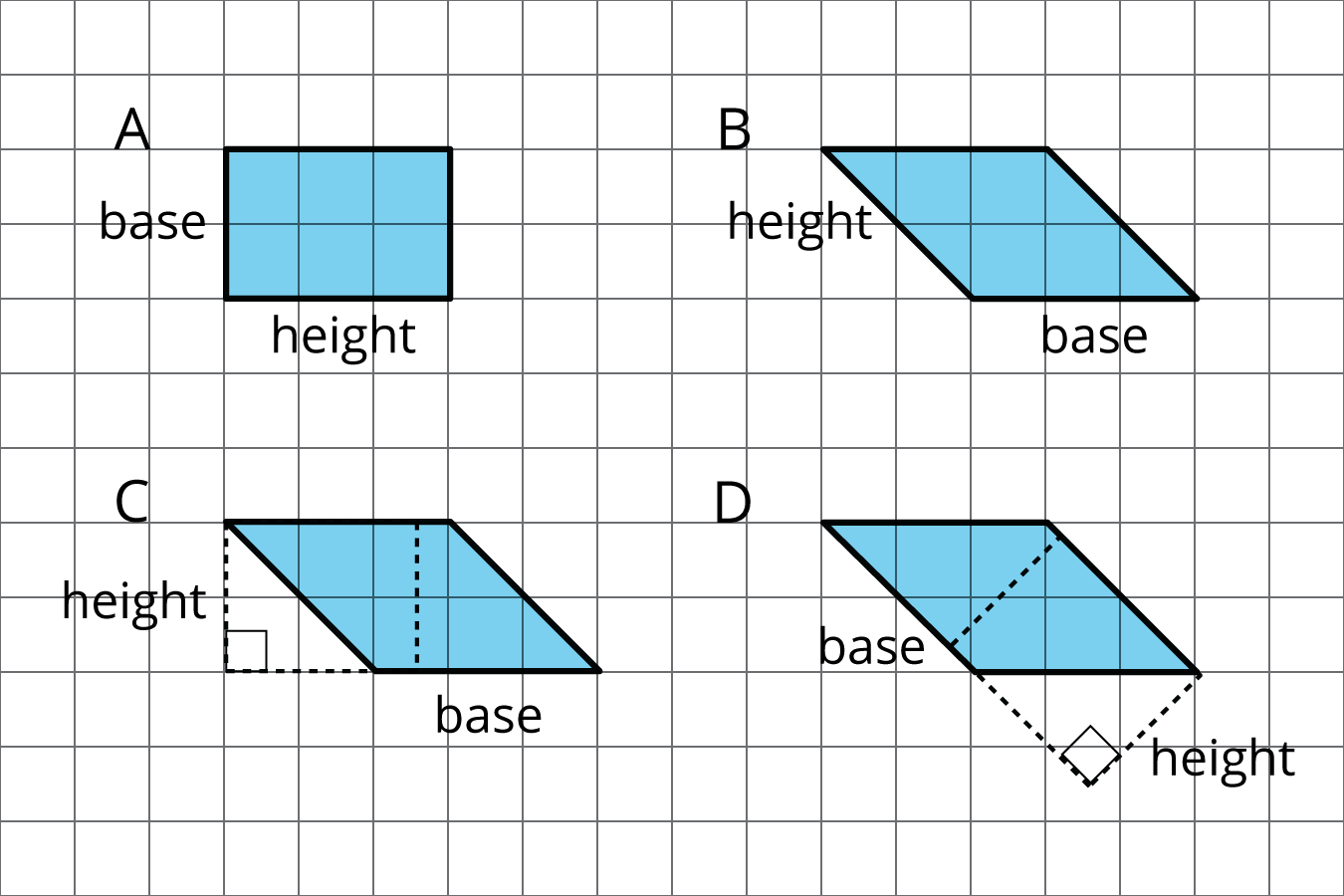
Problem 1

Select all parallelograms that have a correct height labeled for the given base.

Problem 2

The side labeled $b$ has been chosen as the base for this parallelogram.

Draw a segment showing the height corresponding to that base.

Problem 3

Find the area of each parallelogram.

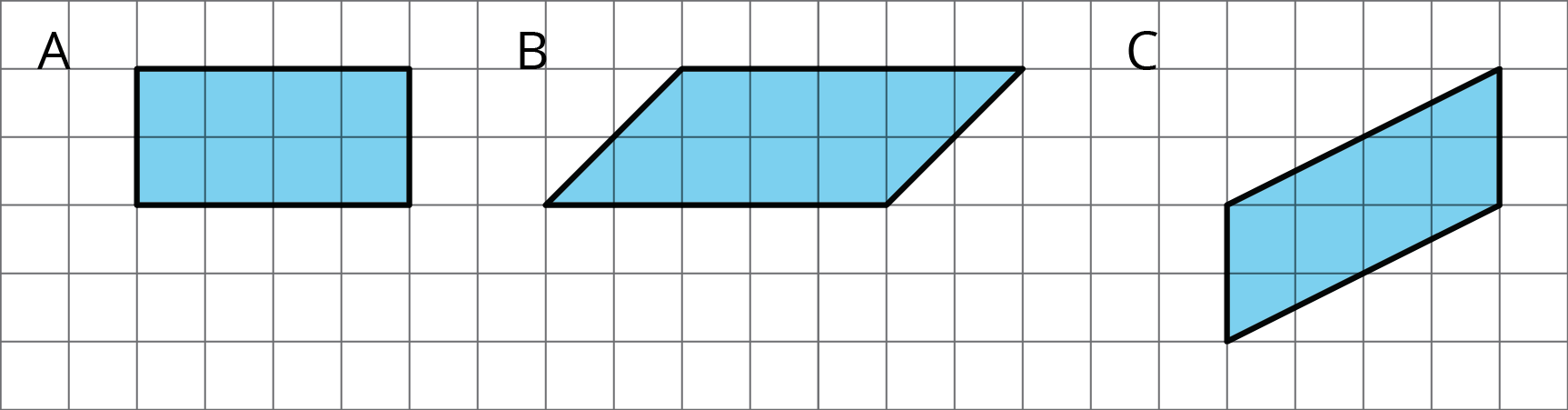
Problem 4

If the side that is 6 units long is the base of this parallelogram, what is its corresponding height?

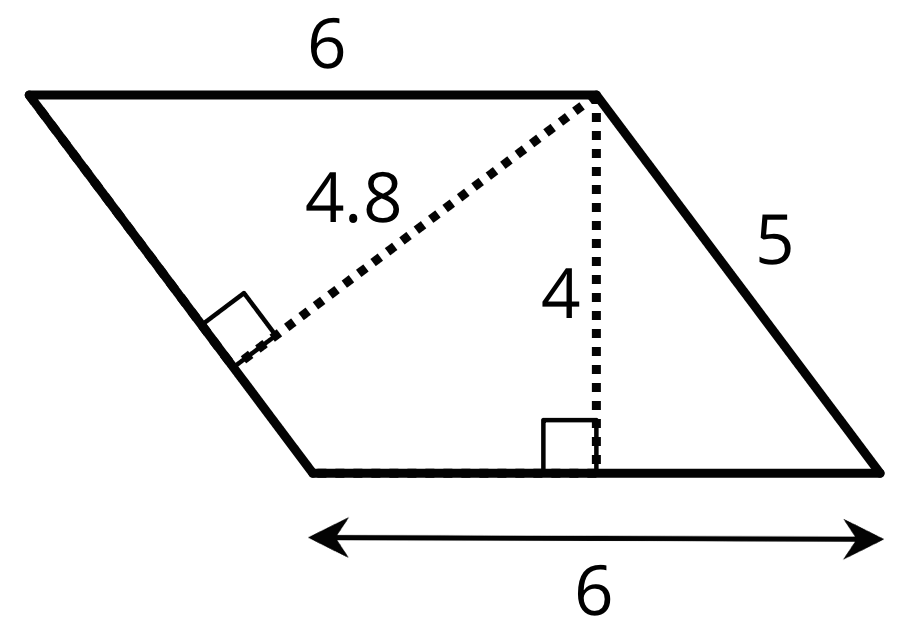
A parallelogram with its bottom and top sides labeled 6 and its right side labeled 5. A dashed line perpendicular to the right side is labeled 4.8, and a dashed line perpendicular to the bottom side is labeled 4.
  1. 6 units
  2. 4.8 units
  3. 4 units
  4. 5 units

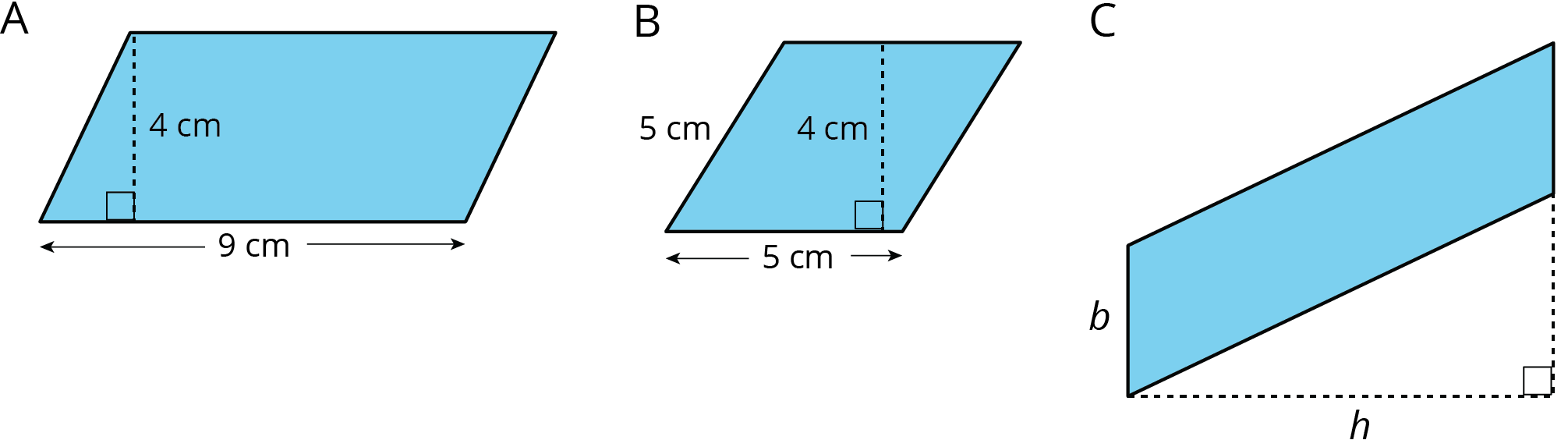
Problem 5

Find the area of each parallelogram.

Problem 6 (from Unit 1, Lesson 4)

Do you agree with each of these statements? Explain your reasoning.

  1. A parallelogram has six sides.
  2. Opposite sides of a parallelogram are parallel.
  3. A parallelogram can have one pair or two pairs of parallel sides. 
  4. All sides of a parallelogram have the same length.
  5. All angles of a parallelogram have the same measure. 

Problem 7 (from Unit 1, Lesson 2)

A square with an area of 1 square meter is decomposed into 9 identical small squares. Each small square is decomposed into two identical triangles.

  1. What is the area, in square meters, of 6 triangles? If you get stuck, draw a diagram.
  2. How many triangles are needed to compose a region that is $1\frac 12$ square meters?

Lesson 6

Problem 1

Which three of these parallelograms have the same area as each other?
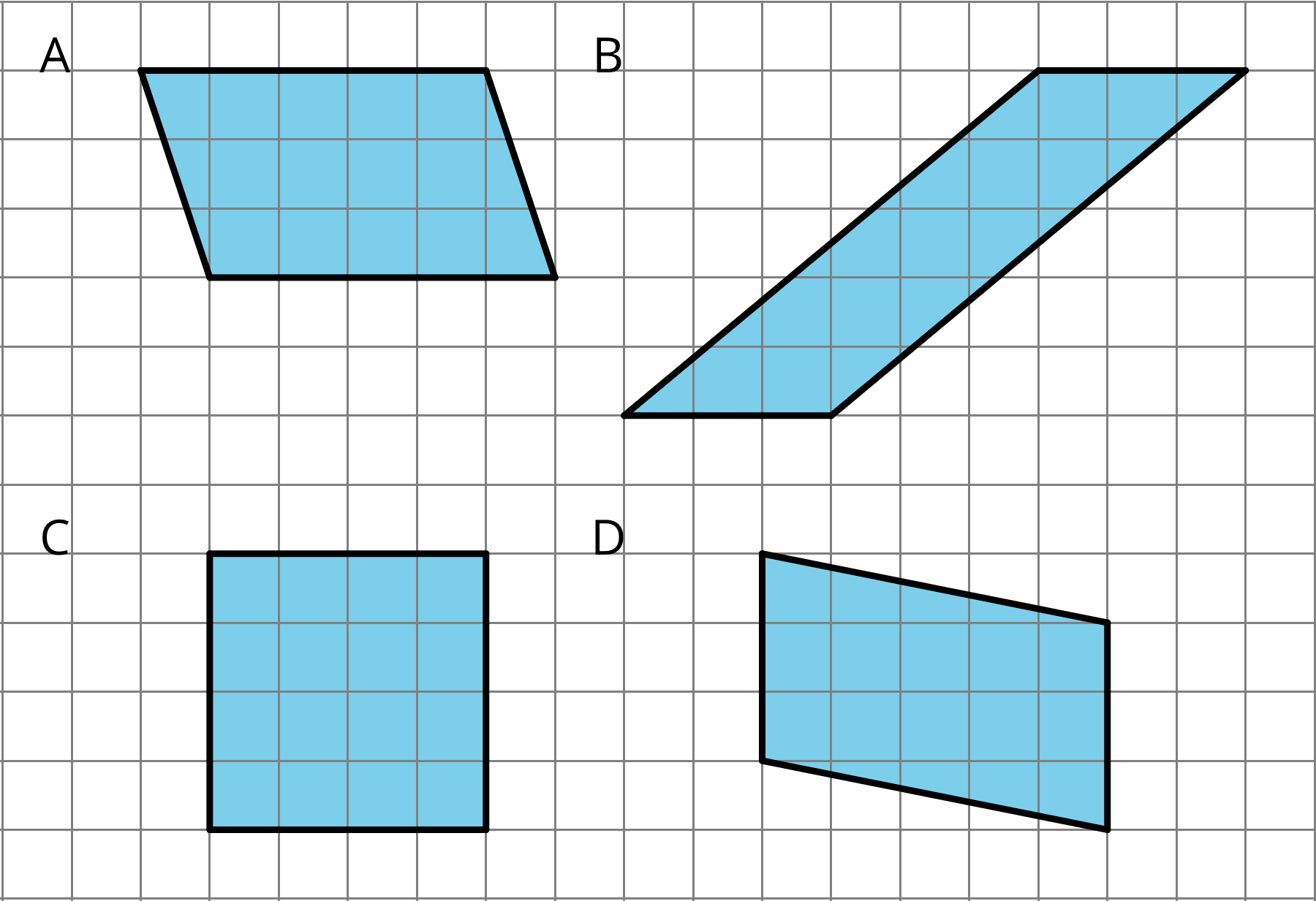
Four parallelograms, labeled A, B, C, and D. In figure A, the top and bottom are each 5 units long, and the sides descend 3 units and move right 1 unit. In figure B, the top and bottom are each 3 units long and the left and right sides ascend 5 units while moving right 6 units. Figure C is a square of 4 units on each side. In figure D, the left and right sides ascend 3 units, and the top and bottom descend 1 unit as they move right 5 units.

Problem 2

Which of the following pairs of base and height produces the greatest area? All measurements are in centimeters.

  1. $b = 4$, $h=3.5$
  2. $b = 0.8$, $h=20$
  3. $b = 6$, $h=2.25$
  4. $b = 10$, $h=1.4$

Problem 3

Here are the areas of three parallelograms. Use them to find the missing length (labeled with a "?") on each parallelogram.

A: 10 square units

B: 21 square units

C: 25 square units

Problem 4

The Dockland Building in Hamburg, Germany is shaped like a parallelogram.

If the length of the building is 86 meters and its height is 55 meters, what is the area of this face of the building?

Problem 5 (from Unit 1, Lesson 5)

Select all segments that could represent a corresponding height if the side $m$ is the base.

A parallelogram with a bottom side labeled m and a right side labeled n. Dashed lines e, f, j, and k are drawn perpendicular to side m, and dashed lines g and h are drawn perpendicular to side n.

Problem 6 (from Unit 1, Lesson 3)

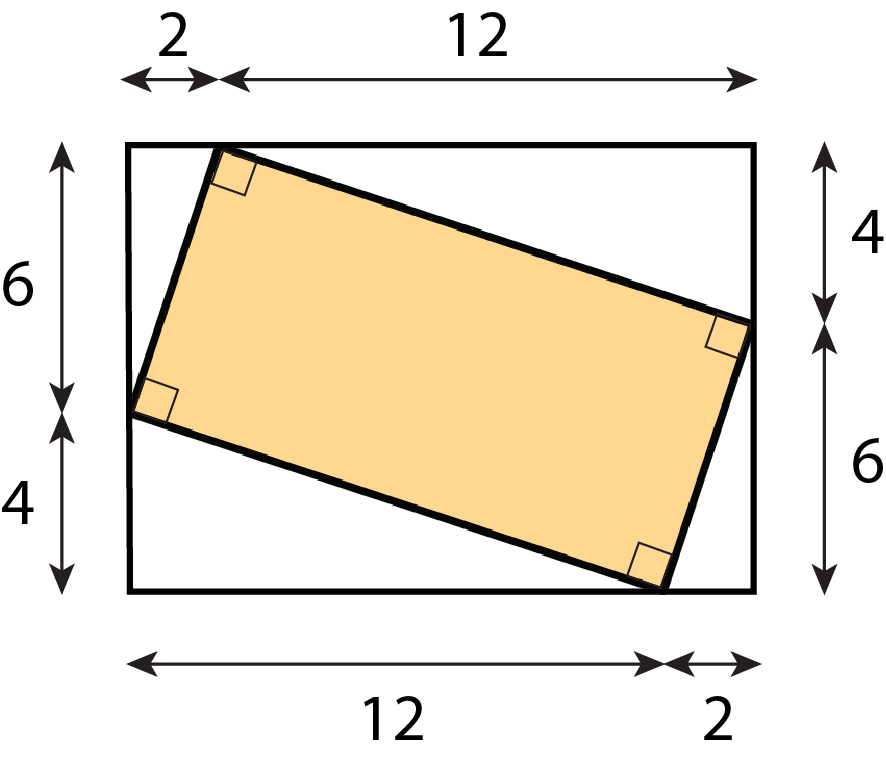
Find the area of the shaded region. All measurements are in centimeters. Show your reasoning.

A shaded rectangle located at an angle within a larger rectangle. The sides of the larger rectangle are divided where the smaller rectangle contacts them. The longer sides are labeled 2 and 12 on each side of the divide, and the shorter sides are labeled 6 and 4 on each side of the divide.

Lesson 7

Problem 1

To decompose a quadrilateral into two identical shapes, Clare drew a dashed line as shown in the diagram.

  1. She said the that two resulting shapes have the same area. Do you agree? Explain your reasoning.

  1. Did Clare partition the figure into two identical shapes? Explain your reasoning.

Problem 2

Triangle R is a right triangle. Can we use two copies of Triangle R to compose a parallelogram that is not a square?

If so, explain how or sketch a solution. If not, explain why not.

Problem 3

 

Two copies of this triangle are used to compose a parallelogram. Which parallelogram cannot be a result of the composition? If you get stuck, consider using tracing paper.

A triangle. The left side of the triangle descends 2 units while moving left by 1 unit. The top side descends 1 unit while moving left 6 units. The bottom side moves up 1 unit while moving left 5 units.
Four parallelograms labeled A, B, C, and D.
 

Problem 4

a. On the grid, draw at least three different quadrilaterals that can each be decomposed into two identical triangles with a single cut (show the cut line). One or more of the quadrilaterals should have non-right angles.

“”

b. Identify the type of each quadrilateral.

Problem 5 (from Unit 1, Lesson 6)

  1. A parallelogram has a base of 9 units and a corresponding height of $\frac23$ units. What is its area?

  2. A parallelogram has a base of 9 units and an area of 12 square units. What is the corresponding height for that base?

  3. A parallelogram has an area of 7 square units. If the height that corresponds to a base is $\frac14$ unit, what is the base?

Problem 6 (from Unit 1, Lesson 5)

Select all segments that could represent a corresponding height if the side $n$ is the base.

A parallelogram with a bottom side labeled m and a right side labeled n. Dashed lines e, f, j, and k are drawn perpendicular to side m, and dashed lines g and h are drawn perpendicular to side n.

Lesson 8

Problem 1

To find the area of this right triangle, Diego and Jada used different strategies. Diego drew a line through the midpoints of the two longer sides, which decomposes the triangle into a trapezoid and a smaller triangle. He then rearranged the two shapes into a parallelogram.

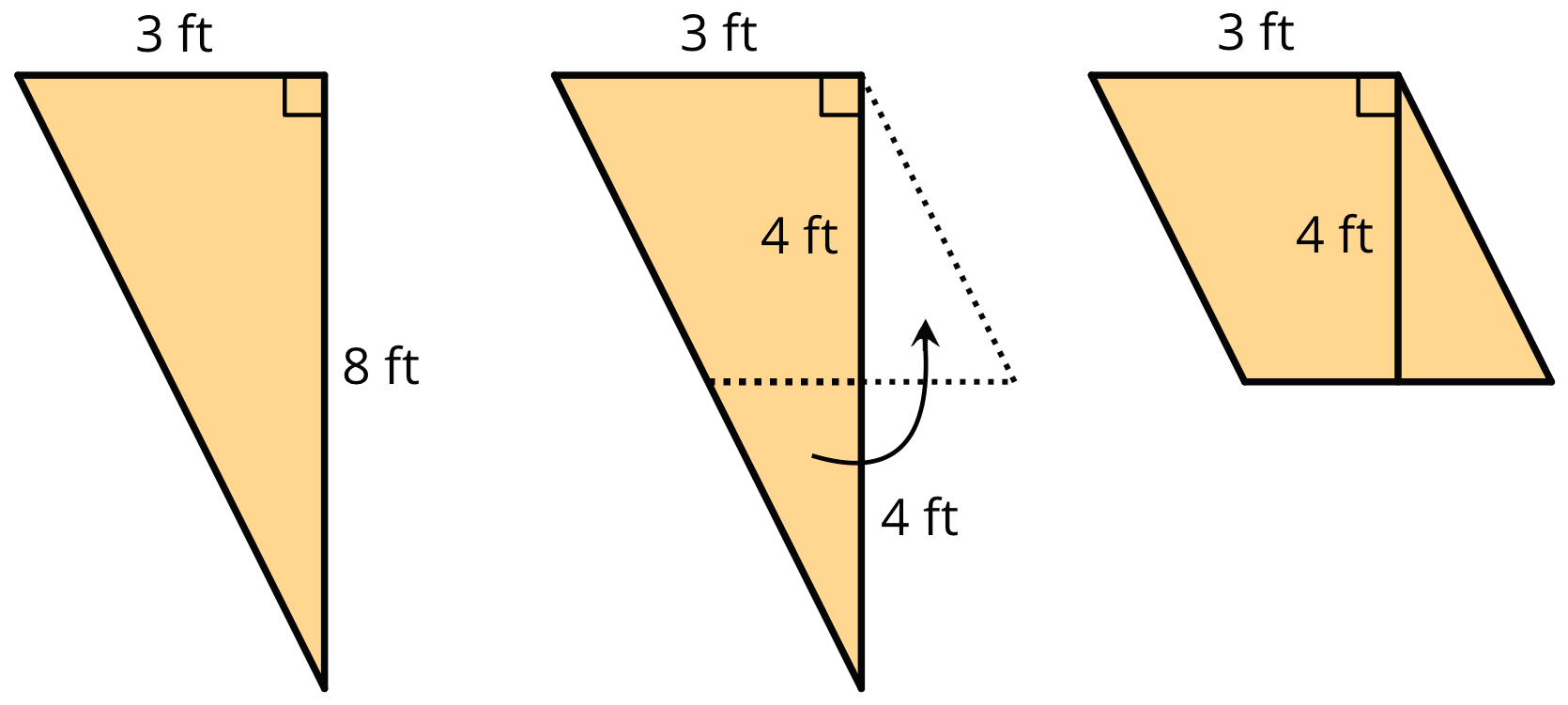
A triangle with one side labeled 3 feet and another side labeled 8 feet. A second image displays the same triangle with a dashed line bisecting the triangle so the side that was labeled 8 feet is now two pieces, each labeled 4 feet. An arrow indicates that the resulting smaller portion is rotated to create a parallelogram with a base of 3 feet and a height of 4 feet.

Jada made a copy of the triangle, rotated it, and lined it up against one side of the original triangle so that the two triangles make a parallelogram.

A triangle with one side labeled 3 feet and another labeled 8 ft. To the left is the same triangle with a copy composed along the 8 feet side to create a parallelogram.
  1. Explain how Diego might use his parallelogram to find the area of the triangle.
  1. Explain how Jada might use her parallelogram to find the area of the triangle.

Problem 2

Find the area of the triangle. Explain or show your reasoning.
a. 
b. 

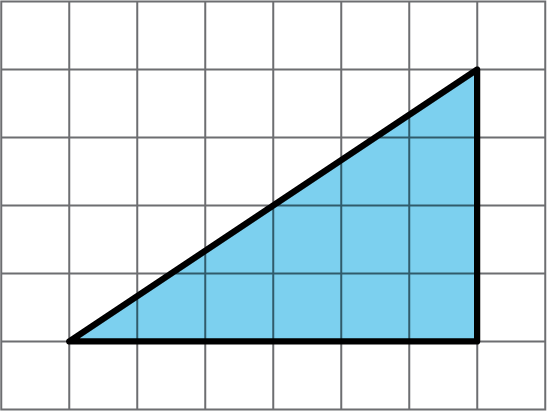
Problem 3

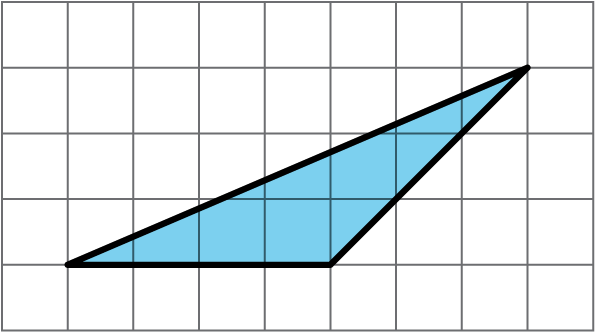
Which of the three triangles has the greatest area? Show your reasoning.

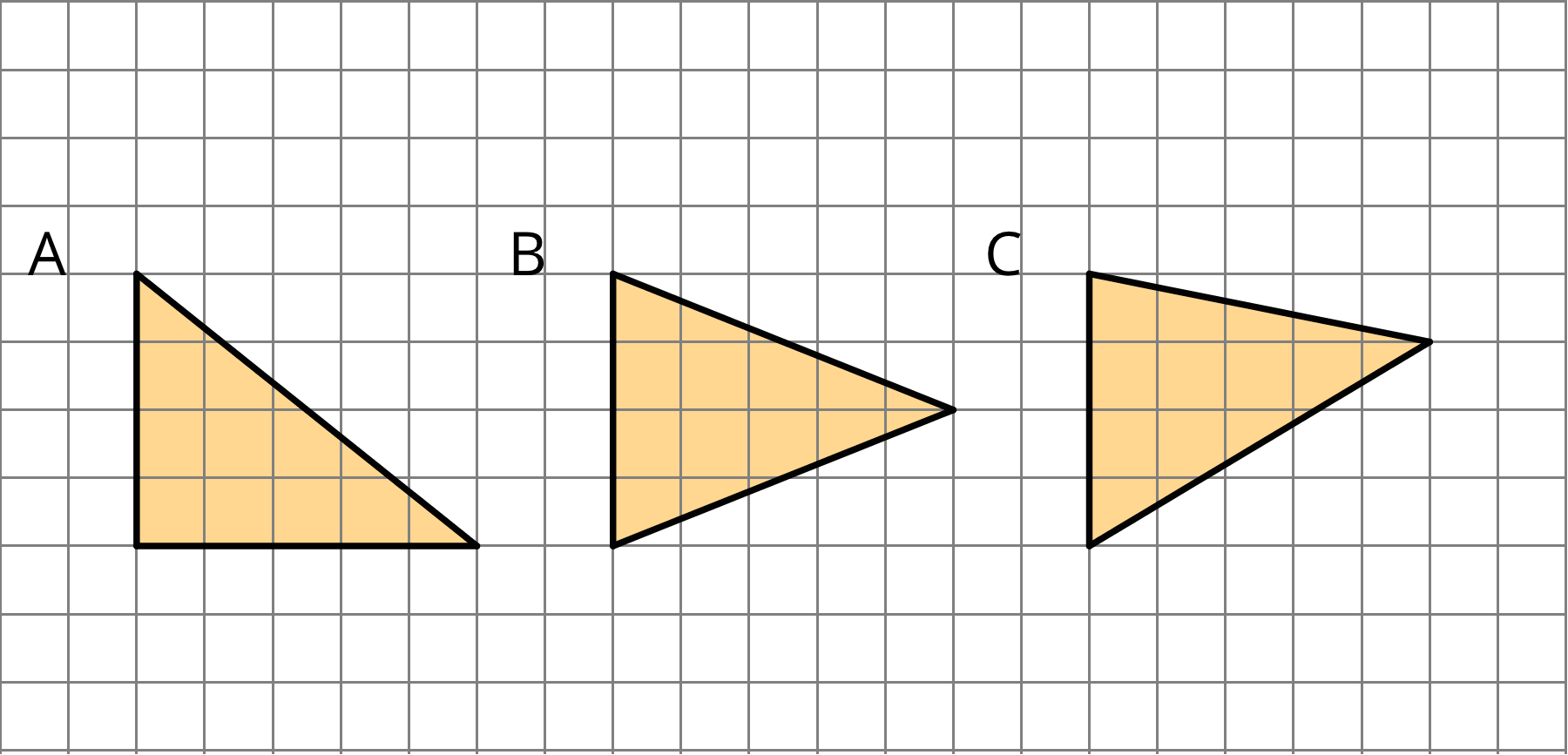
Three triangles labeled A, B, and C. Triangle A is a right triangle with a base of 5 and a height of 4. Triangle B has a base of 4 and a height of 5. Triangle C has a base of 4 and a height of 5.
 

If you get stuck, use what you know about the area of parallelograms to help you.

 

Problem 4 (from Unit 1, Lesson 7)

Draw an identical copy of each triangle such that the two copies together form a parallelogram. If you get stuck, consider using tracing paper.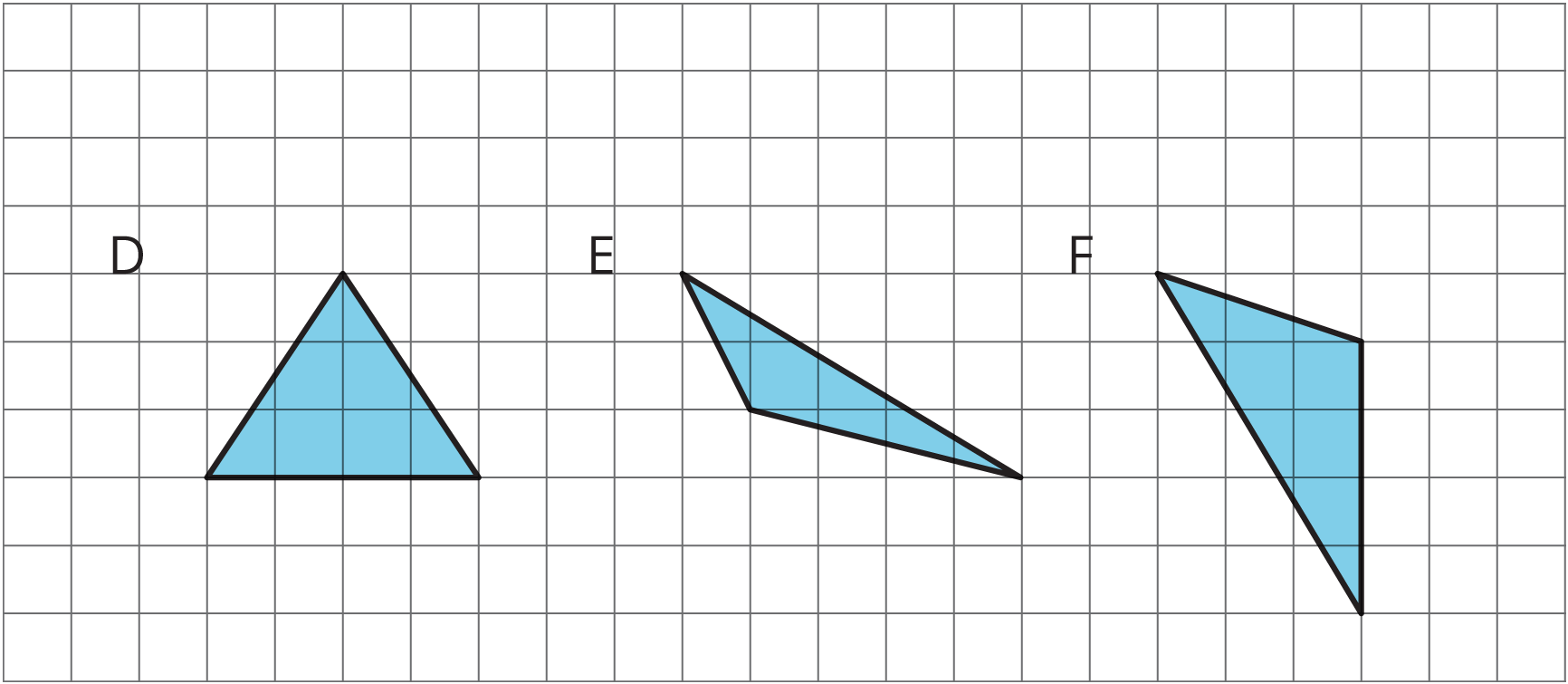Three triangles labeled D, E, and F.

Problem 5 (from Unit 1, Lesson 6)

  1. A parallelogram has a base of 3.5 units and a corresponding height of 2 units. What is its area?

  2. A parallelogram has a base of 3 units and an area of 1.8 square units. What is the corresponding height for that base?

  3. A parallelogram has an area of 20.4 square units. If the height that corresponds to a base is 4 units, what is the base?

Lesson 9

Problem 1

 

Select all drawings in which a corresponding height $h$ for a given base $b$ is correctly identified.

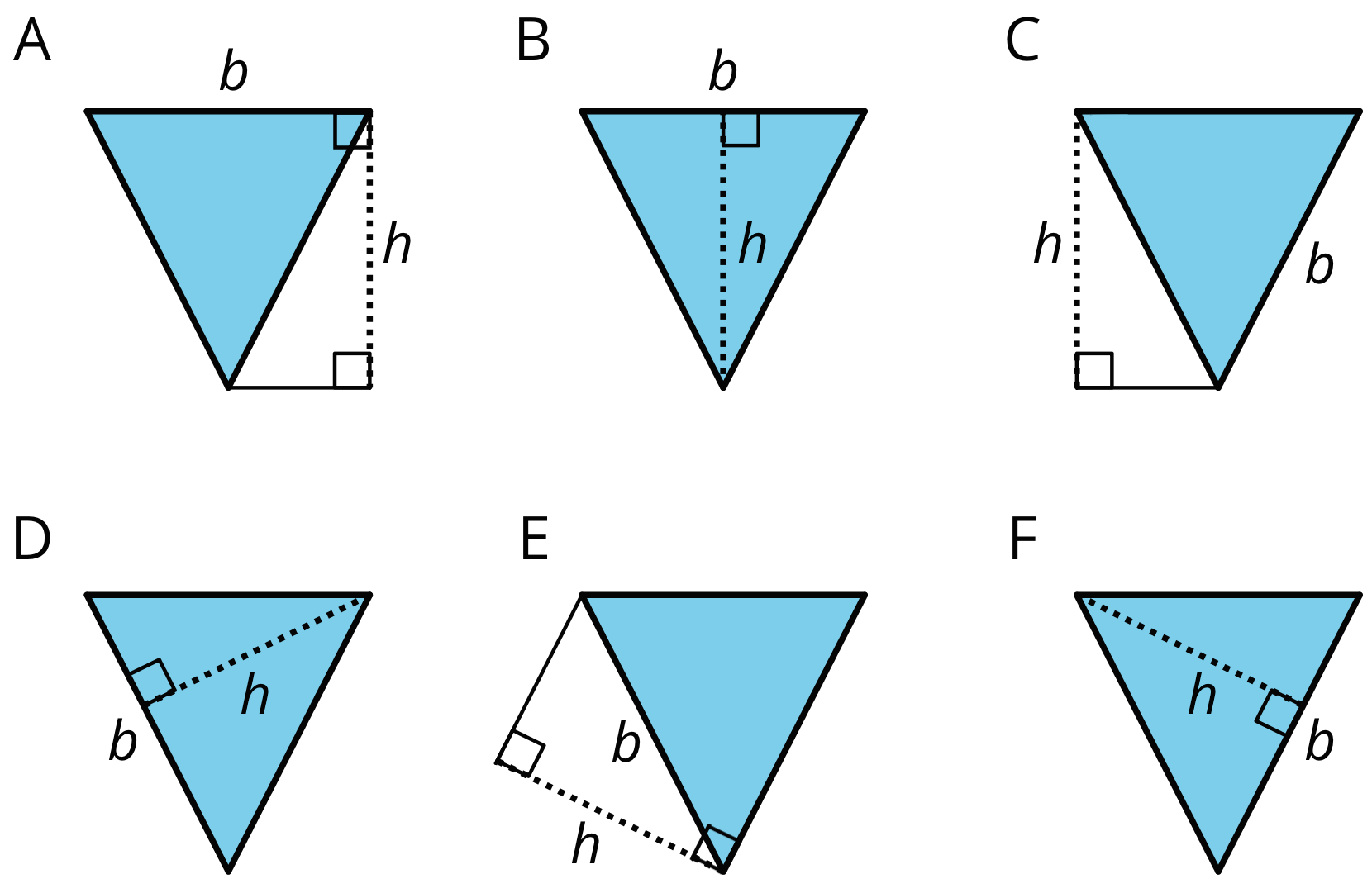
Six images of the same triangle, labeled A, B, C, D, E, and F. On triangle A, the top side is labeled “b” and a dashed line extending straight down from the right vertex islabeled “h”. On triangle B the top side is labeled “b” and a dashed line extends from the center of the top side to the opposite vertex labeled “h”. On triangle C, the right side is labeled “b” and a dashed line extends from the right top vertex straight down to the level of the bottom vertex. On triangle D the left side is labeled “b” and a perpendicular line labeled “h” extends to the opposite vertex. On triangle E, the right side is labeled “b” and a dashed line labeled “h” extends out from the bottom vertex at a right angle to the left side. On triangle F, the right side is labeled “b” and a perpendicular dashed line labeled “h” extends from the side labeled “b” and extends to the opposite vertex.

Problem 2

For each triangle, a base and its corresponding height are labeled.

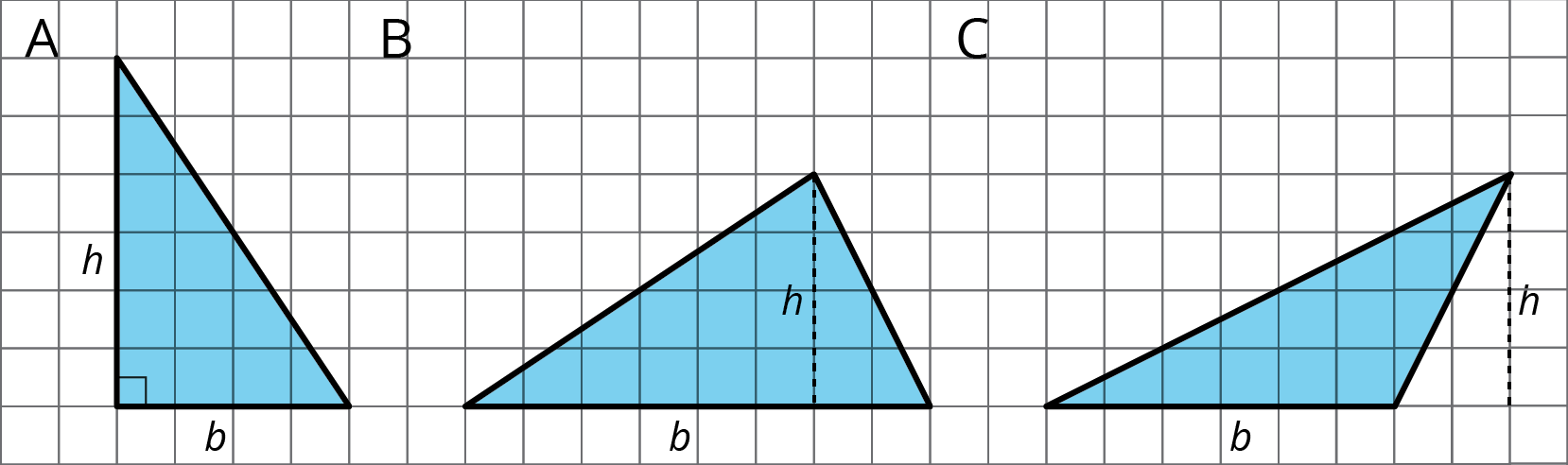
a. Find the area of each triangle.

b. How is the area related to the base and its corresponding height?

Problem 3

Here is a right triangle. Name a corresponding height for each base.

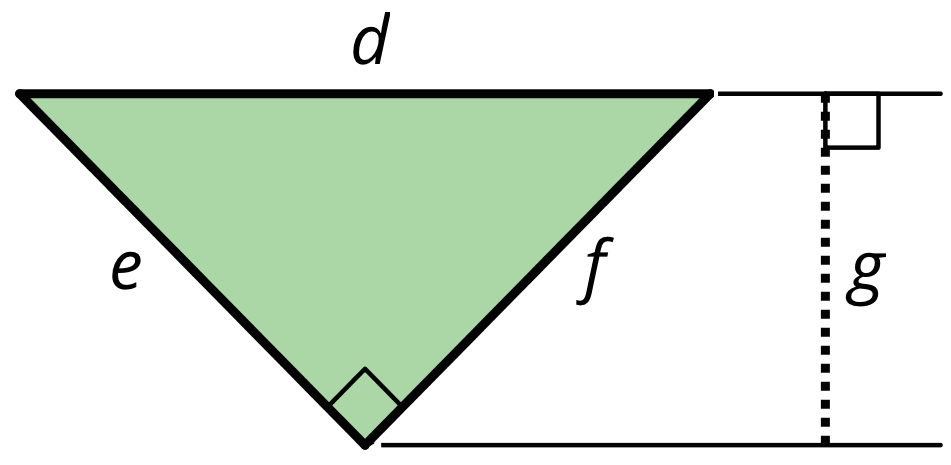
A triangle with sides labeled d, e, and f. The angle opposite side D is a right angle. A segment labeled g is perpendicular to side d and extends to the opposite vertex.
  1. Side $d$
  2. Side $e$
  3. Side $f$

Problem 4 (from Unit 1, Lesson 8)

Find the area of the shaded triangle. Show your reasoning.

A square with a shaded triangle contained inside it. The left and bottom sides of the square are labeled six, and the right side is labeled 2 above the point where vertex of the shaded triangle meets the side, and 4 below the point where the vertex meets the side.

Problem 5 (from Unit 1, Lesson 7)

Andre drew a line connecting two opposite corners of a parallelogram. Select all true statements about the triangles created by the line Andre drew.

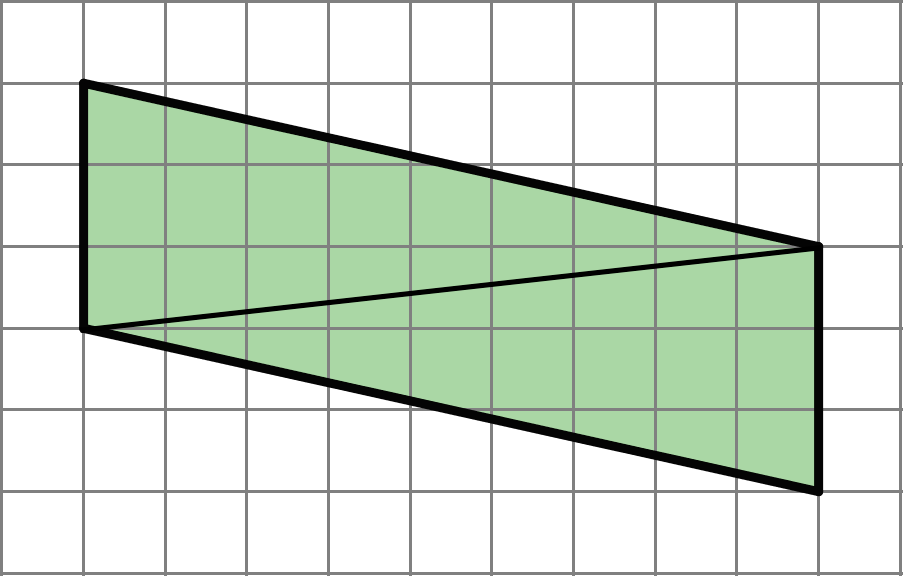
A parallelogram with a line connecting two opposite corners. The parallelogram has a base of 3 units and a height of 9 units.

  1. Each triangle has two sides that are 3 units long.
  2. Each triangle has a side that is the same length as the diagonal line.
  3. Each triangle has one side that is 3 units long.
  4. When one triangle is placed on top of the other and their sides are aligned, we will see that one triangle is larger than the other.
  5. The two triangles have the same area as each other.

Problem 6 (from Unit 1, Lesson 3)

Here is an octagon.

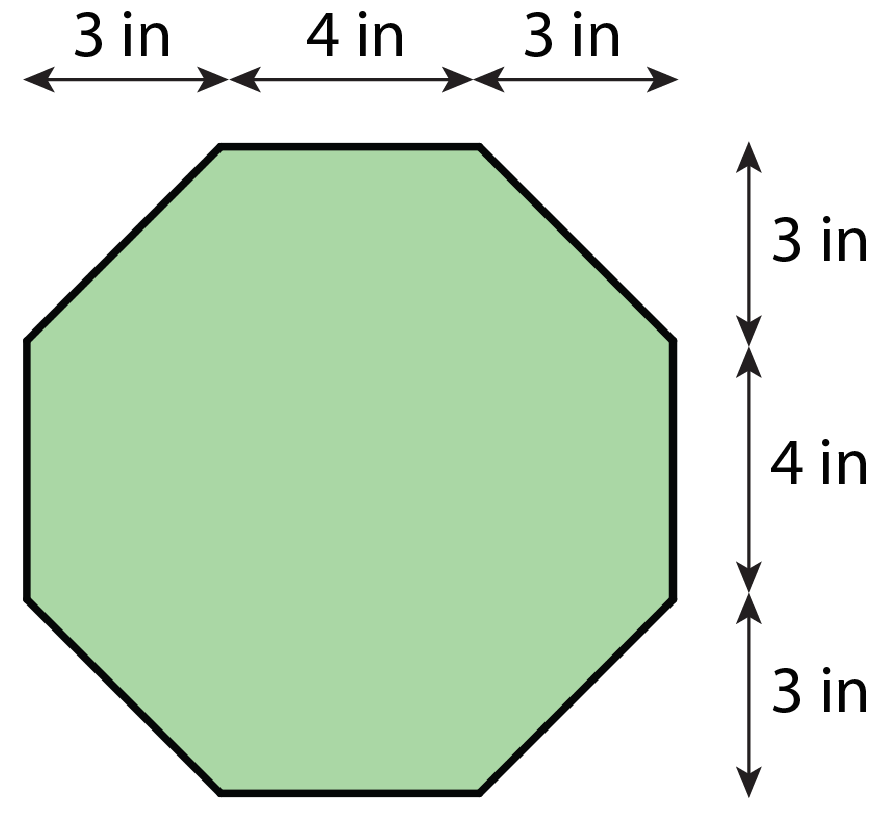
An octagon with straight sides that are 4 inches long, and angled sides that are both 3 inches high and 3 inches wide.
  1. While estimating the area of the octagon, Lin reasoned that it must be less than 100 square inches. Do you agree? Explain your reasoning.
  2. Find the exact area of the octagon. Show your reasoning.

Lesson 10

Problem 1

For each triangle, a base is labeled $b$. Draw a line segment that shows its corresponding height. Use an index card to help you draw a straight line.

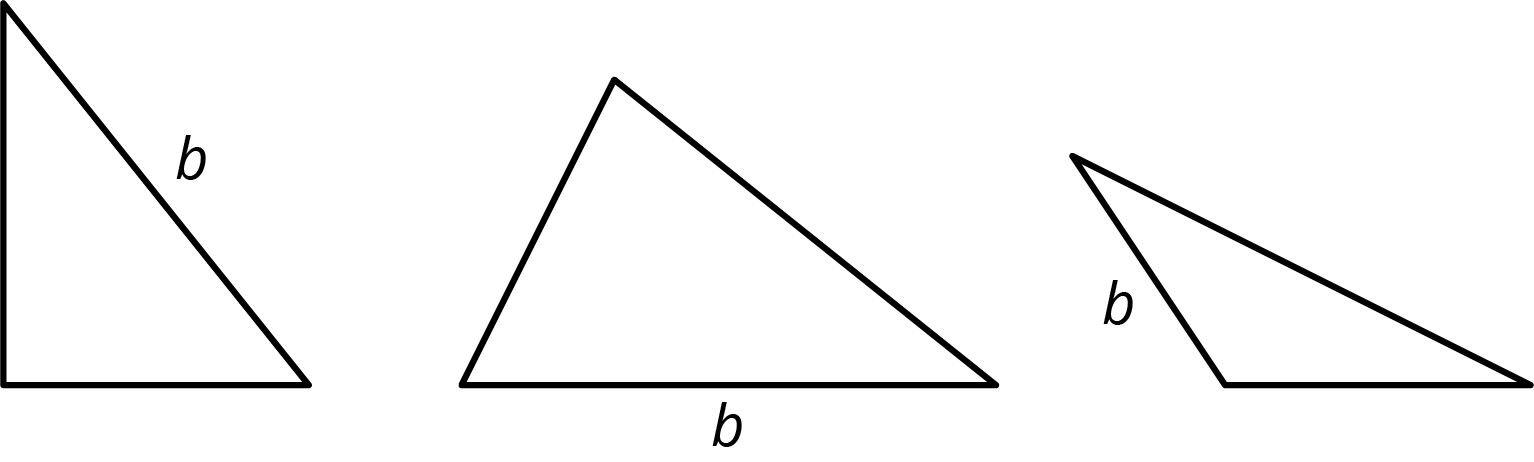
Problem 2

Select all triangles that have an area of 8 square units. Explain how you know.

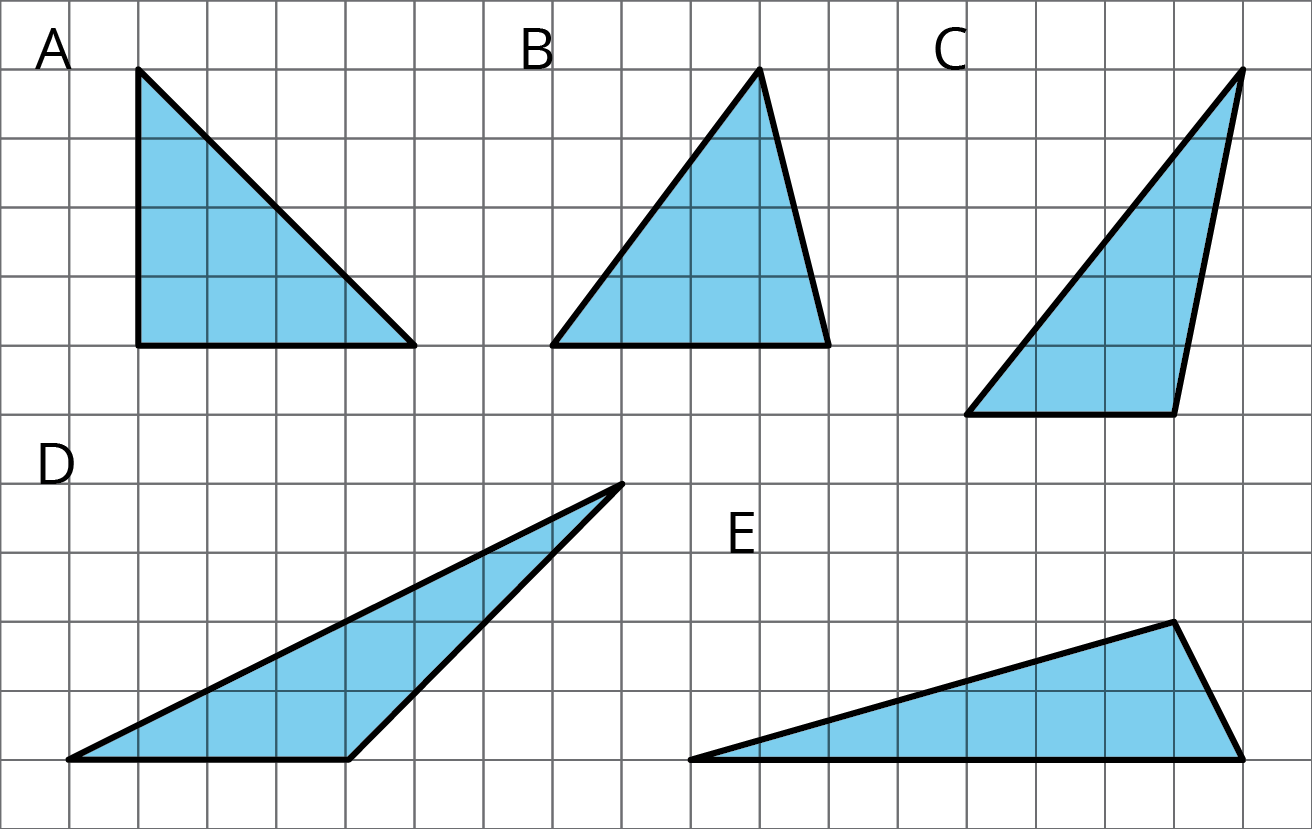
Problem 3

Find the area of the triangle. Show your reasoning.

If you get stuck, carefully consider which side of the triangle to use as the base.

 

Problem 4

Can side $d$ be the base for this triangle? If so, which length would be the corresponding height? If not, explain why not.

Problem 5 (from Unit 1, Lesson 3)

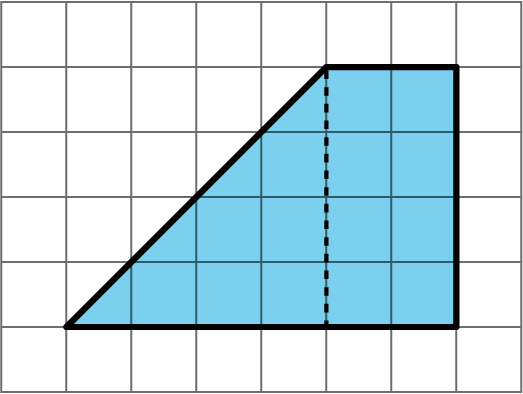
Find the area of this shape. Show your reasoning.

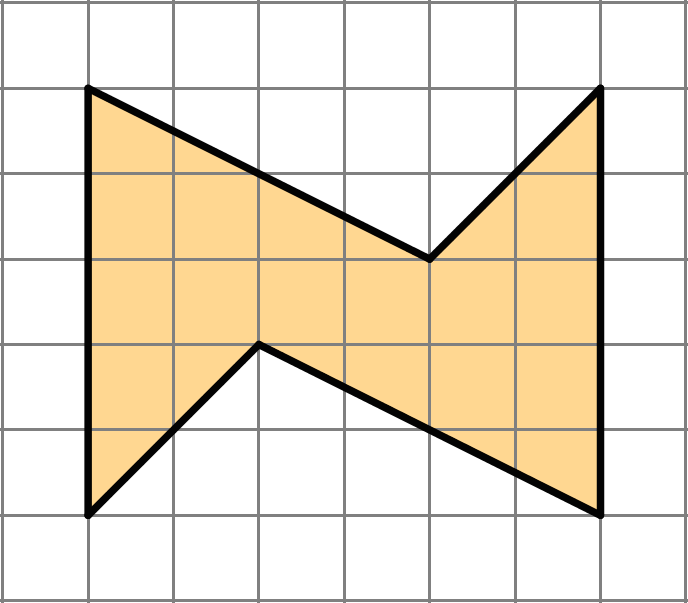
A shape with six sides. There are two vertical sides measuring five units, two angled sides that fall 2 units over 4 units and two sides that fall 2 units over 2 units.

Problem 6 (from Unit 1, Lesson 6)

On the grid, sketch two different parallelograms that have equal area. Label a base and height of each and explain how you know the areas are the same.

“”

Lesson 11

Problem 1

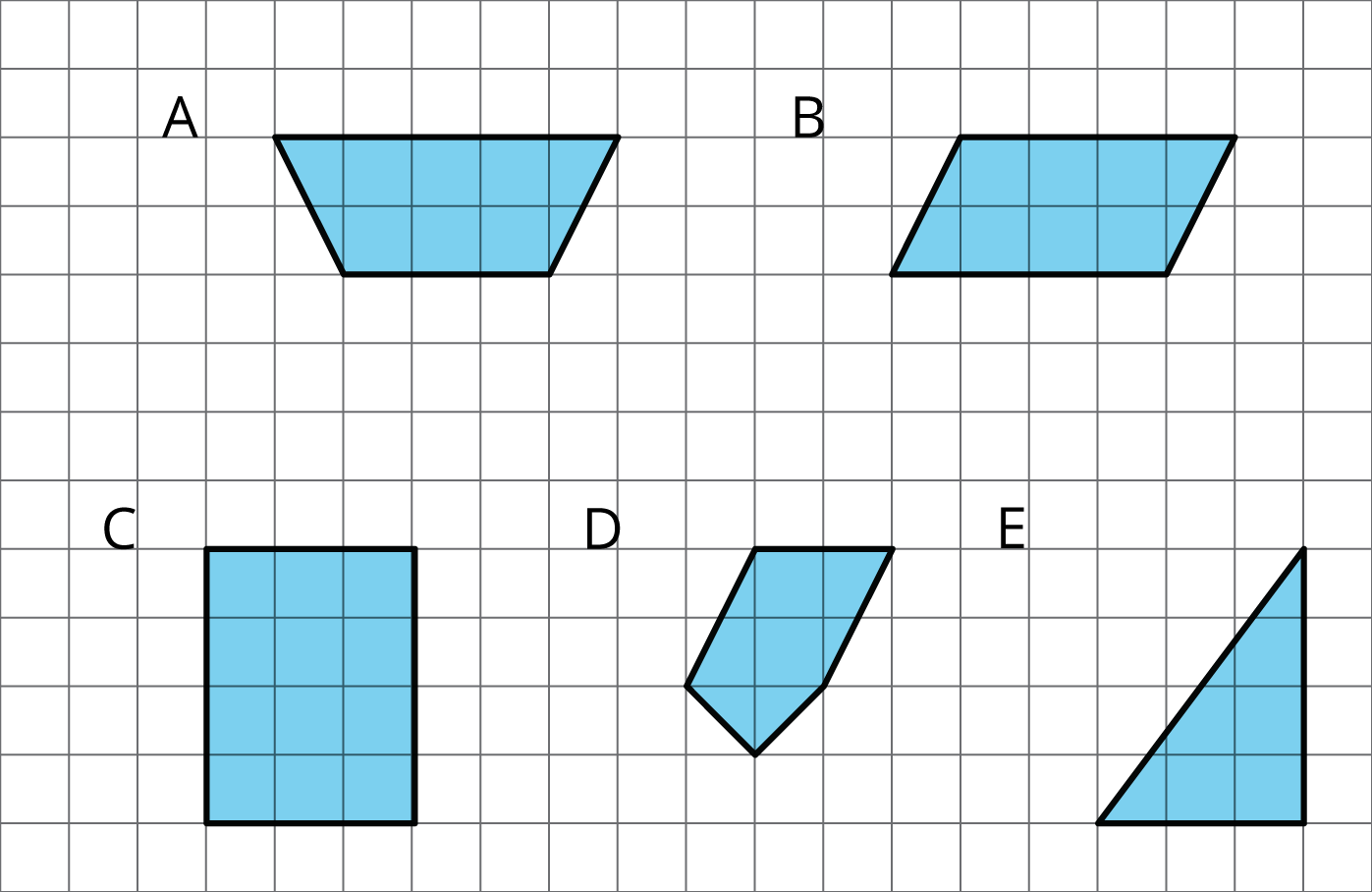
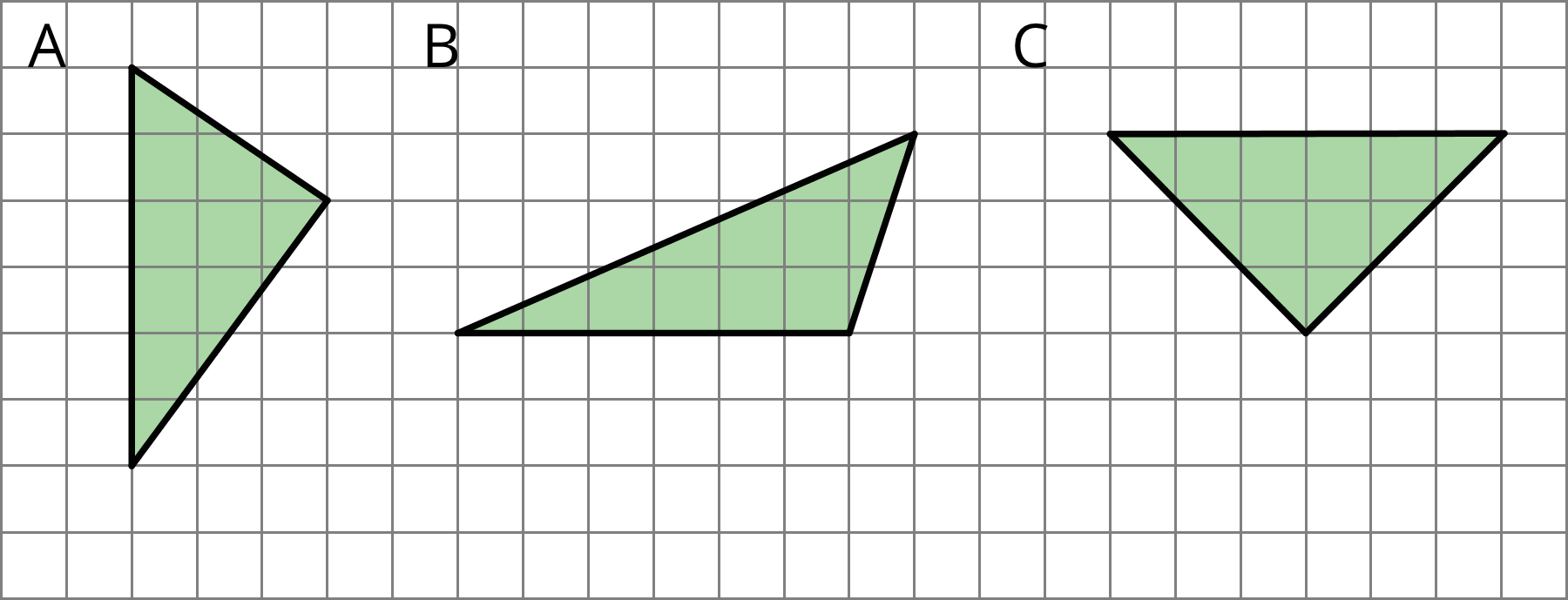
Select all the polygons.

Problem 2

Mark each vertex with a large dot. How many edges and vertices does this polygon have?

Problem 3

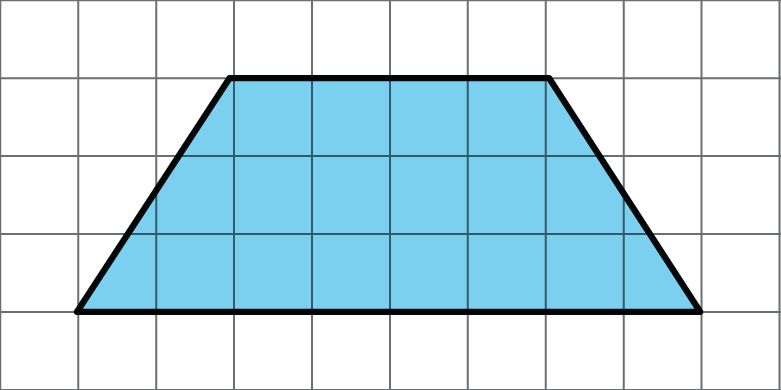
Find the area of this trapezoid. Explain or show your strategy.

 

Problem 4

Lin and Andre used different methods to find the area of a regular hexagon with 6-inch sides. Lin decomposed the hexagon into six identical triangles. Andre decomposed the hexagon into a rectangle and two triangles.

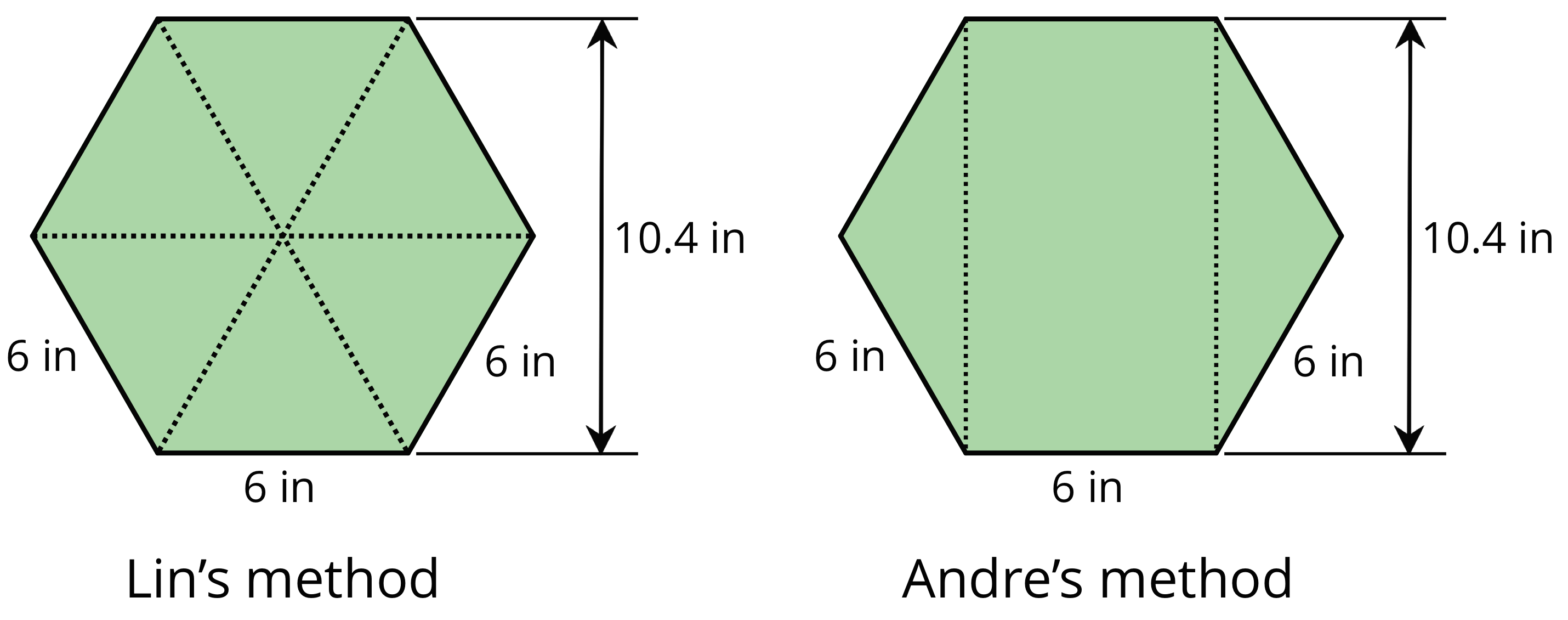
Two identical hexagons labeled “Lin’s method” and “Andre’s method”. Each hexagon has three sides labeled 6 inches and an arrow indicating total height labeled 10.4 inches. “Lin’s method” is divided into six equal triangles, and Andre’s method is decomposed into a rectangle made of lines extending from one side to the opposite side, with a triangle on either side of the rectangle.

Find the area of the hexagon using each person’s method. Show your reasoning.

Problem 5 (from Unit 1, Lesson 9)

  1. Identify a base and a corresponding height that can be used to find the area of this triangle. Label the base $b$ and the corresponding height $h$.

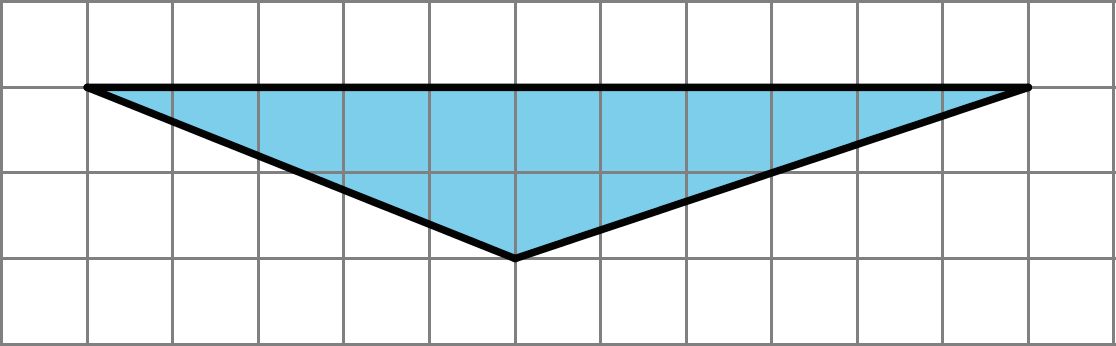
    A triangle that has two vertices 11 units apart from one another horizontally, and a third vertex that is 2 units below the horizontal line and five units right of the left vertex and 6 units right of the left vertex.

    2. Find the area of the triangle. Show your reasoning.

Problem 6 (from Unit 1, Lesson 10)

On the grid, draw three different triangles with an area of 12 square units. Label the base and height of each triangle.

Lesson 12

Problem 1

What is the surface area of this rectangular prism?

  1. 16 square units
  2. 32 square units
  3. 48 square units
  4. 64 square units

Problem 2

Which description can represent the surface area of this trunk?

  1. The number of square inches that cover the top of the trunk.
  2. The number of square feet that cover all the outside faces of the trunk.
  3. The number of square inches of horizontal surface inside the trunk.
  4. The number of cubic feet that can be packed inside the trunk.

Problem 3

Which figure has a greater surface area?

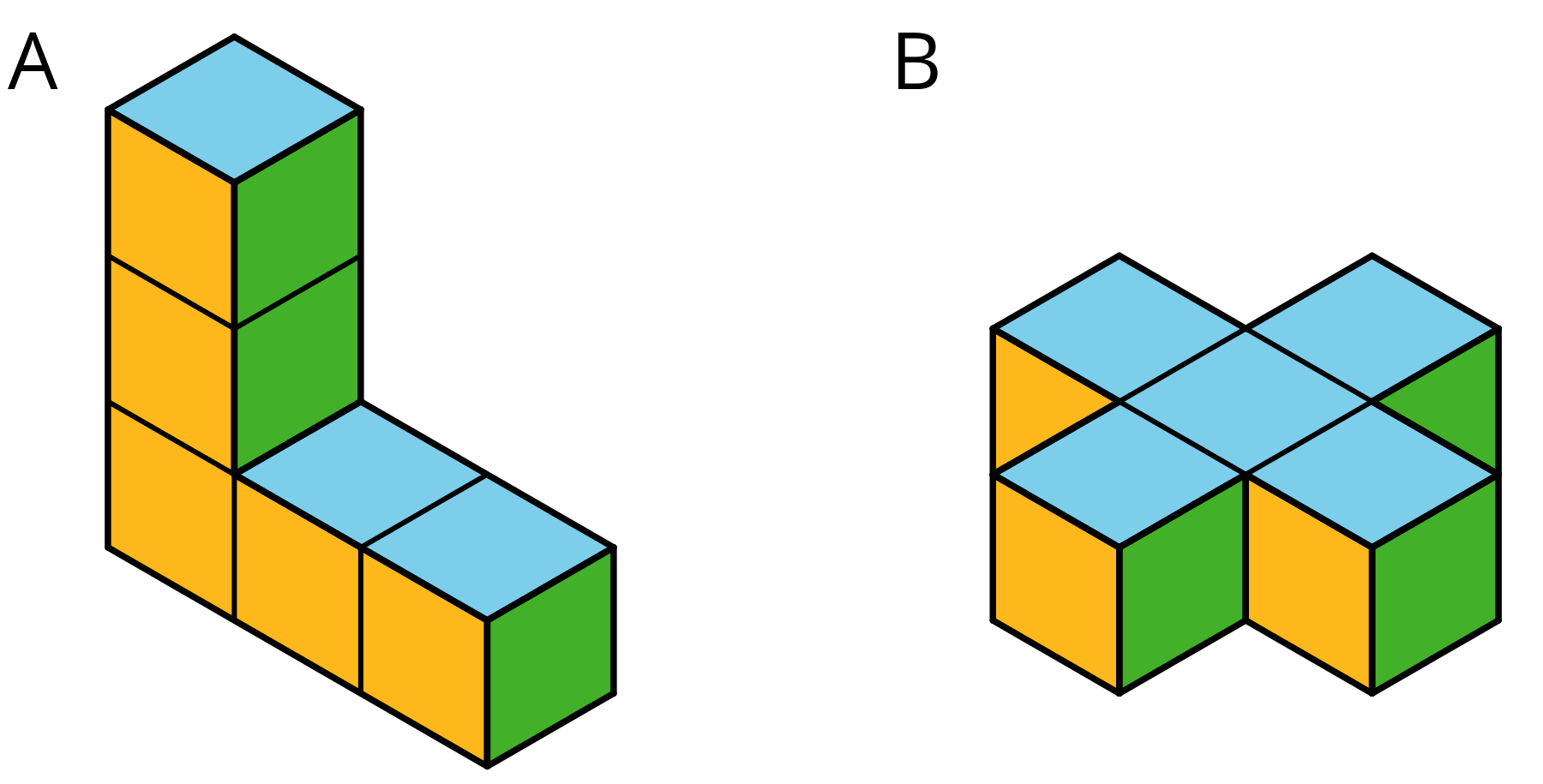
Problem 4

A rectangular prism is 4 units high, 2 units wide, and 6 units long. What is its surface area in square units? Explain or show your reasoning.

Problem 5 (from Unit 1, Lesson 9)

Draw an example of each of the following triangles on the grid.

“”
  1. A right triangle with an area of 6 square units.
  2. An acute triangle with an area of 6 square units.
  3. An obtuse triangle with an area of 6 square units.

Problem 6 (from Unit 1, Lesson 10)

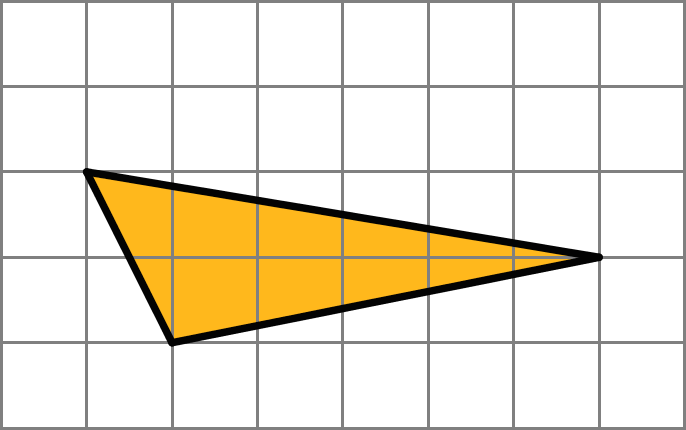
Find the area of triangle $MOQ$ in square units. Show your reasoning.

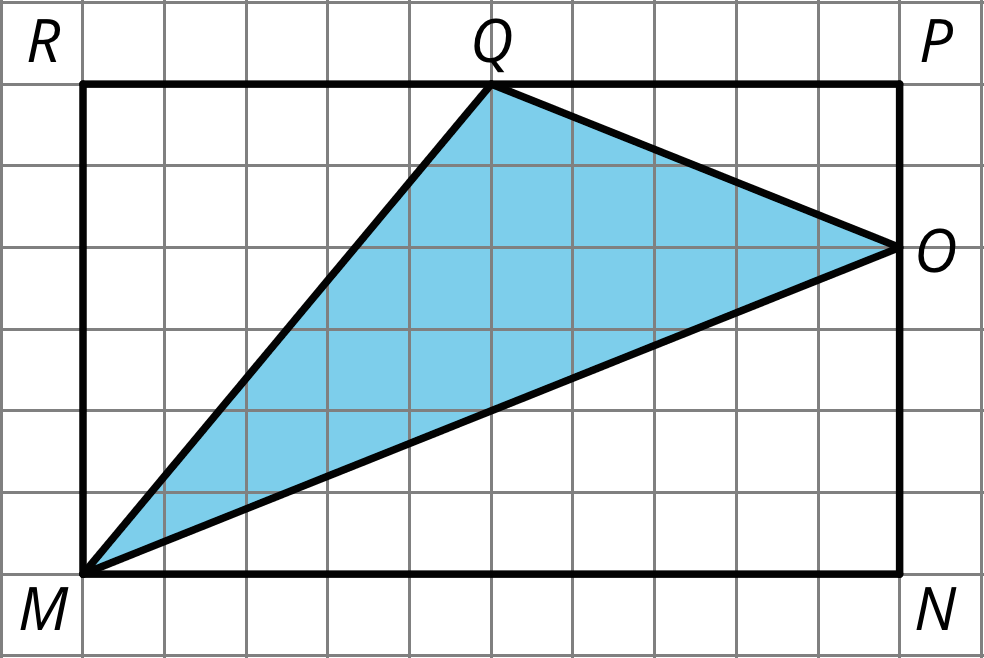
A triangle with vertices labeled M, Q, and P. Triangle MQP is enclosed in a rectangle MRPN. Sides MR and PN of the rectangle are six units high, and sides RP and MN of the rectangle are 10 units long. Vertex Q is five units across side RP, and vertex O is 2 units down on side PN.

 

Problem 7 (from Unit 1, Lesson 3)

Find the area of this shape. Show your reasoning.

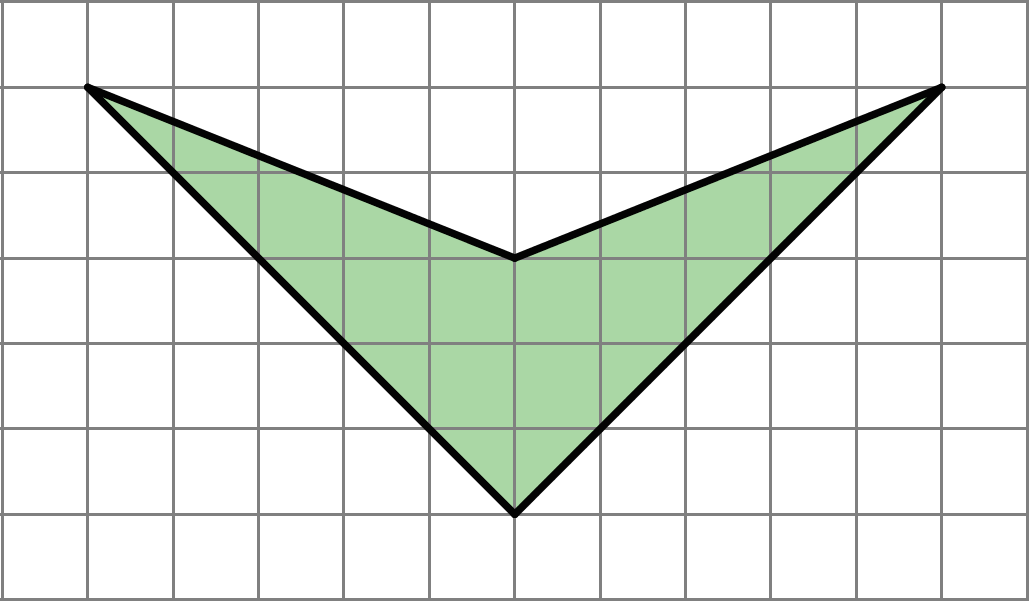
A four-sided shape on a grid, with two sides that drop 5 units as they cross 5 units and meet at a right angle, and two sides that drop two units as they cross 5 units.

 

Lesson 13

Problem 1

 

Select all the polyhedra.

Problem 2

  1. Is this polyhedron a prism, a pyramid, or neither? Explain how you know.
  1. How many faces, edges, and vertices does it have?

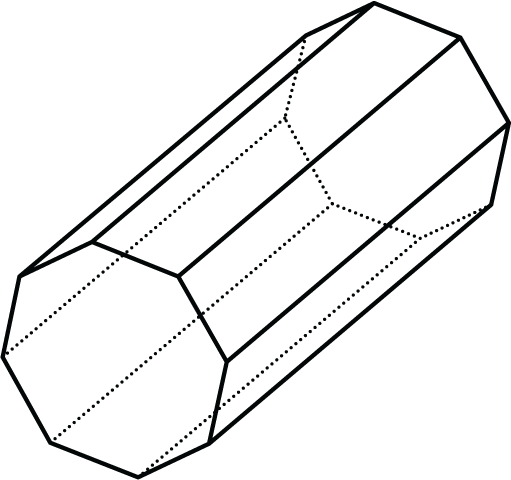
Problem 3

Tyler said this net cannot be a net for a square prism because not all the faces are squares.

Do you agree with Tyler's statement? Explain your reasoning.

 

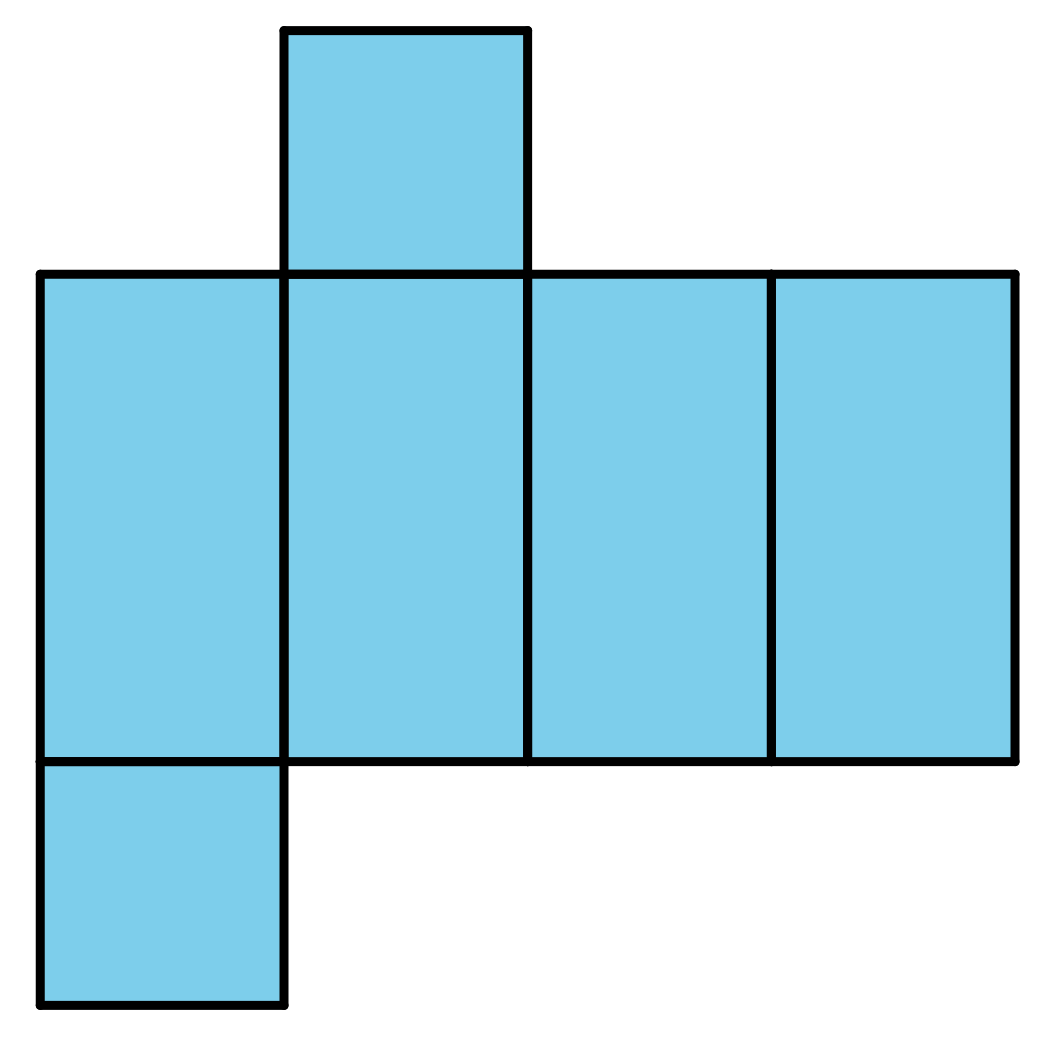
Problem 4 (from Unit 1, Lesson 8)

Explain why each of the following triangles has an area of 9 square units.

Three triangles labeled A, B, and, C. Each triangle has a bas of 6 units and a height of 3 units.

Problem 5 (from Unit 1, Lesson 9)

  1. A parallelogram has a base of 12 meters and a height of 1.5 meters. What is its area?
  2. A triangle has a base of 16 inches and a height of $\frac18$ inches. What is its area?
  3. A parallelogram has an area of 28 square feet and a height of 4 feet. What is its base?
  4. A triangle has an area of 32 square millimeters and a base of 8 millimeters. What is its height?

Problem 6 (from Unit 1, Lesson 3)

Find the area of the shaded region. Show or explain your reasoning.

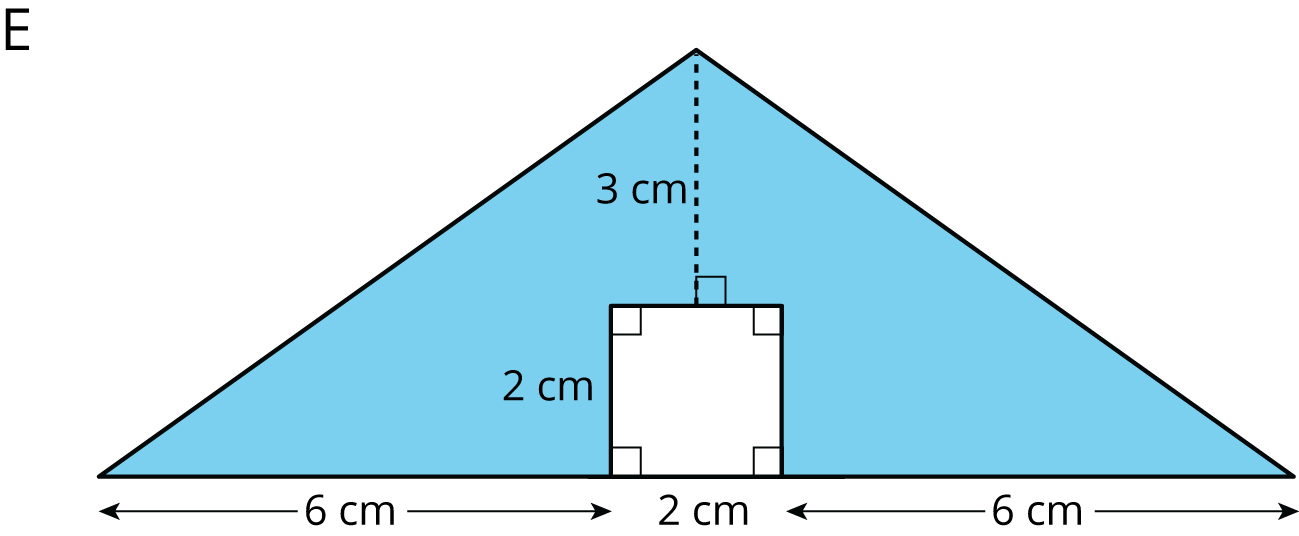
Lesson 14

Problem 1

Can the following net be assembled into a cube? Explain how you know. Label parts of the net with letters or numbers if it helps your explanation.

Problem 2

  1. What polyhedron can be assembled from this net? Explain how you know.
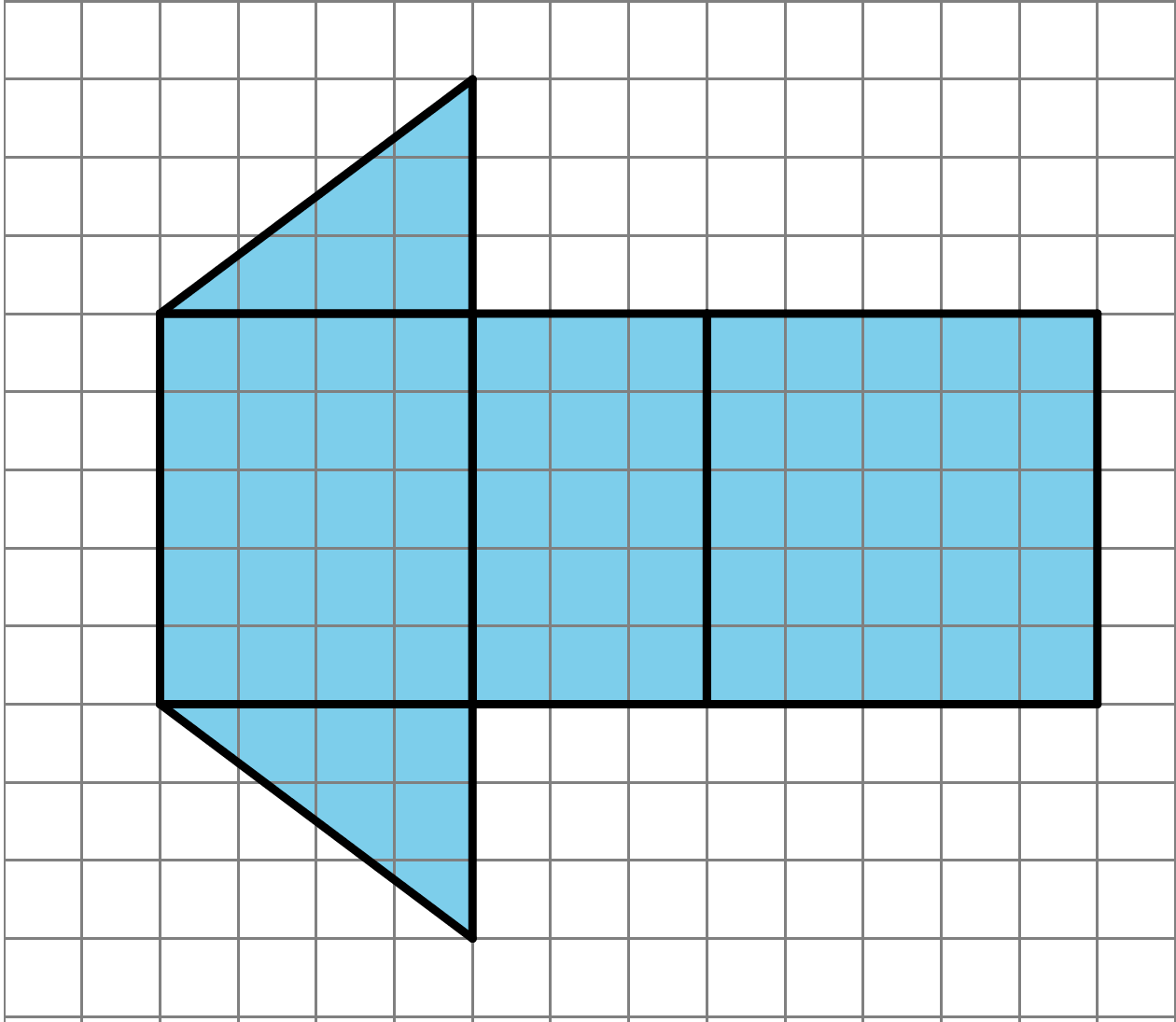
  1. Find the surface area of this polyhedron. Show your reasoning.

Problem 3

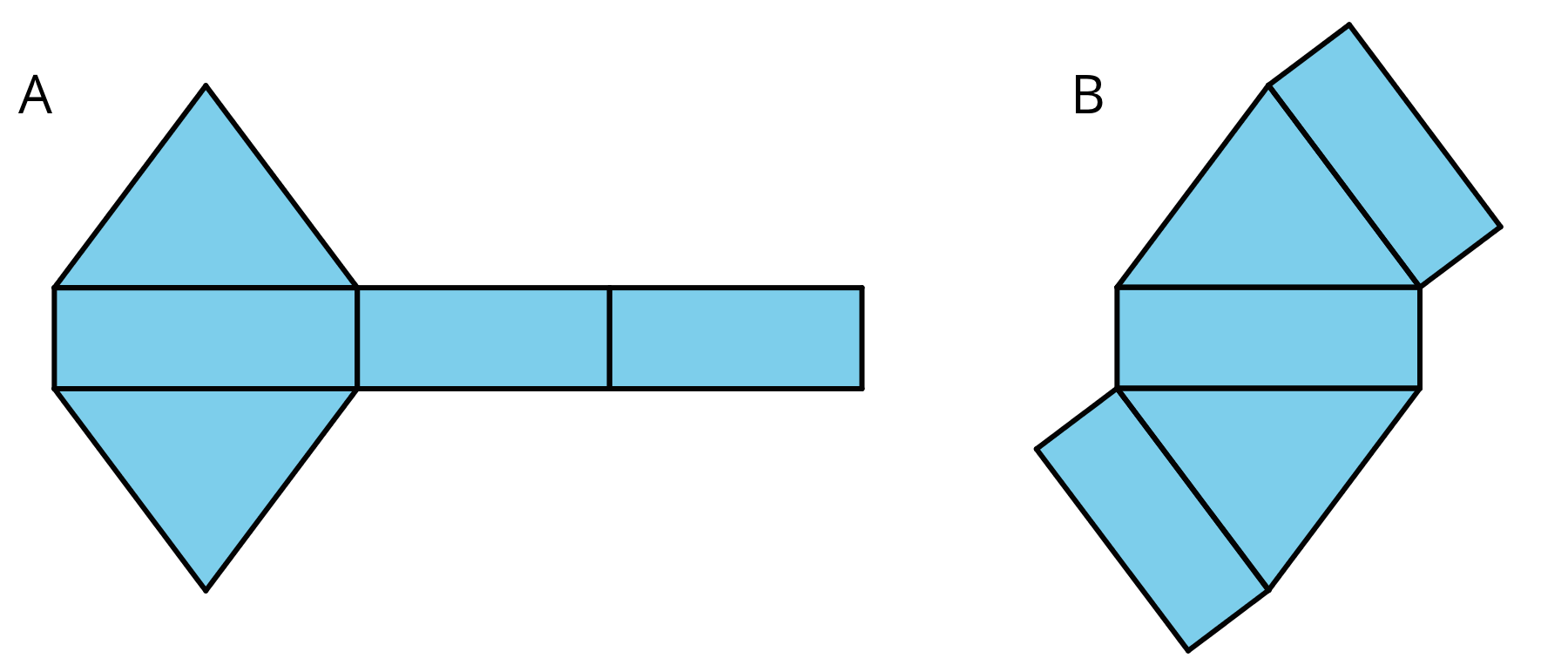
Here are two nets. Mai said that both nets can be assembled into the same triangular prism. Do you agree? Explain or show your reasoning.

Problem 4 (from Unit 1, Lesson 13)

Here are two three-dimensional figures.

Tell whether each of the following statements describes Figure A, Figure B, both, or neither.

  1. This figure is a polyhedron.
  2. This figure has triangular faces.
  3. There are more vertices than edges in this figure.
  4. This figure has rectangular faces.
  1. This figure is a pyramid.
  2. There is exactly one face that can be the base for this figure.
  3. The base of this figure is a triangle.
  4. This figure has two identical and parallel faces that can be the base.

Problem 5 (from Unit 1, Lesson 12)

Select all units that can be used for surface area. Explain why the others cannot be used for surface area.

  1. square meters
  2. feet
  3. centimeters
  4. cubic inches
  5. square inches
  6. square feet

Problem 6 (from Unit 1, Lesson 11)

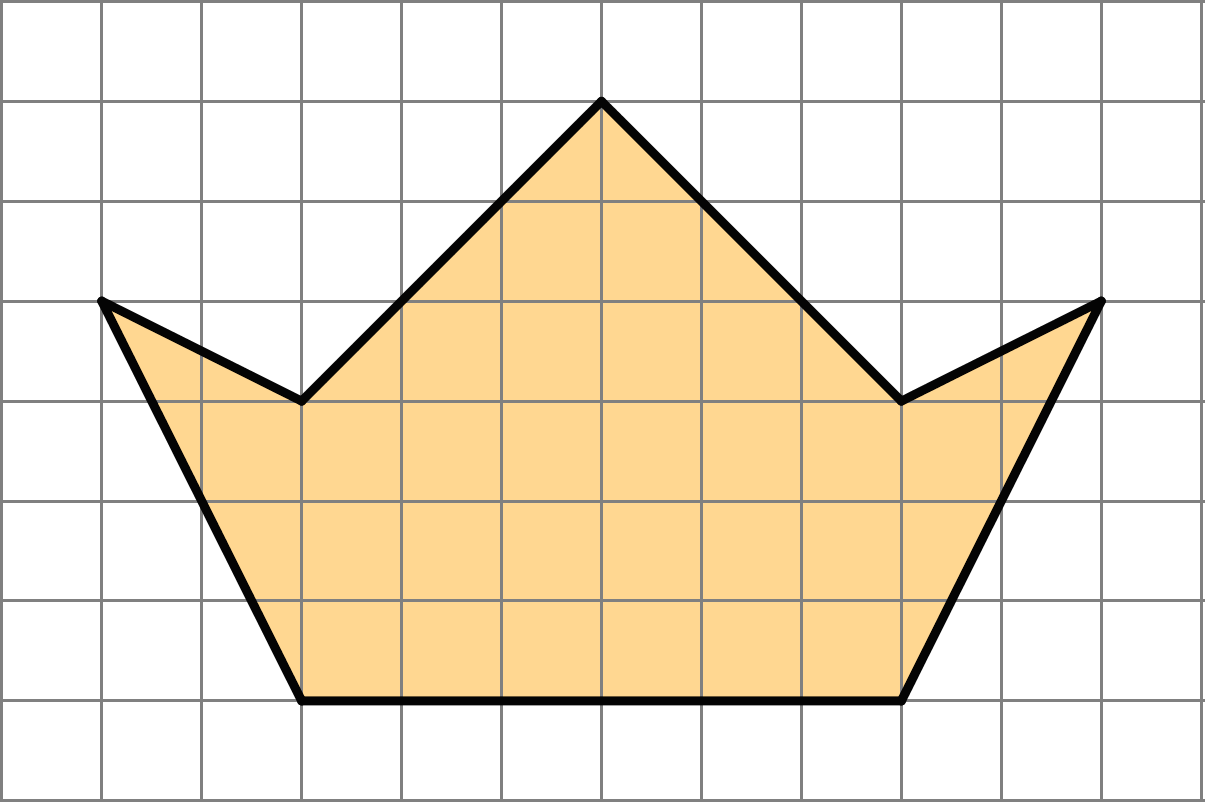
Find the area of this polygon. Show your reasoning.

An image of a 7-sided polygon. The bottom side of the polygon is six units long, and extends out to a total width of 10 units, and a central height of 6 units.

 

Lesson 15

Problem 1

Jada drew a net for a polyhedron and calculated its surface area. 

  1. What polyhedron can be assembled from this net?
  2. Jada made some mistakes in her area calculation. What were the mistakes?

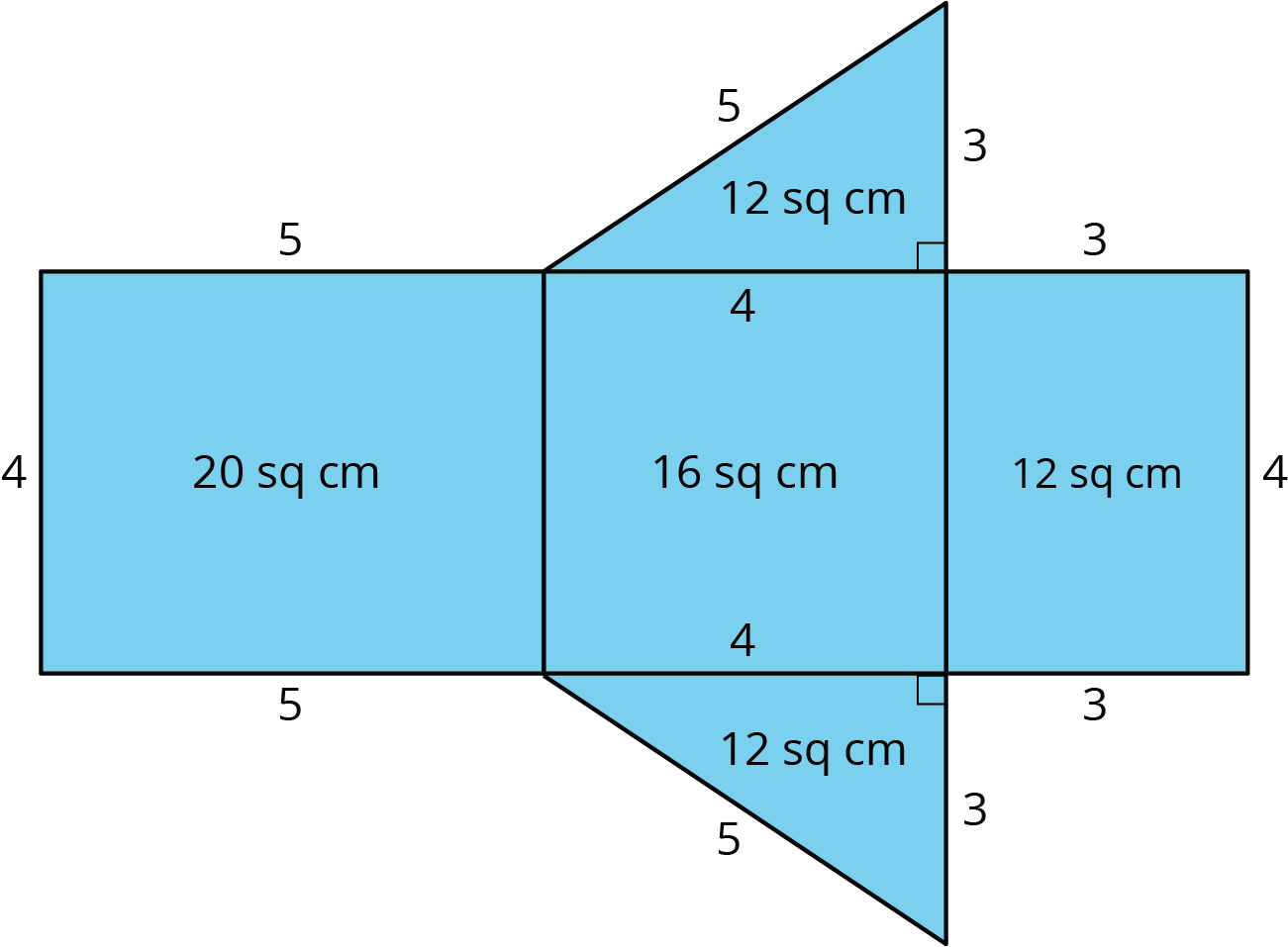
  1. Find the surface area of the polyhedron. Show your reasoning.

Problem 2

A cereal box is 8 inches by 2 inches by 12 inches. What is its surface area? Show your reasoning. If you get stuck, consider drawing a sketch of the box or its net and labeling the edges with their measurements.

Problem 3 (from Unit 1, Lesson 12)

Twelve cubes are stacked to make this figure.

  1. What is its surface area?
  2. How would the surface area change if the top two cubes are removed?
 

Problem 4

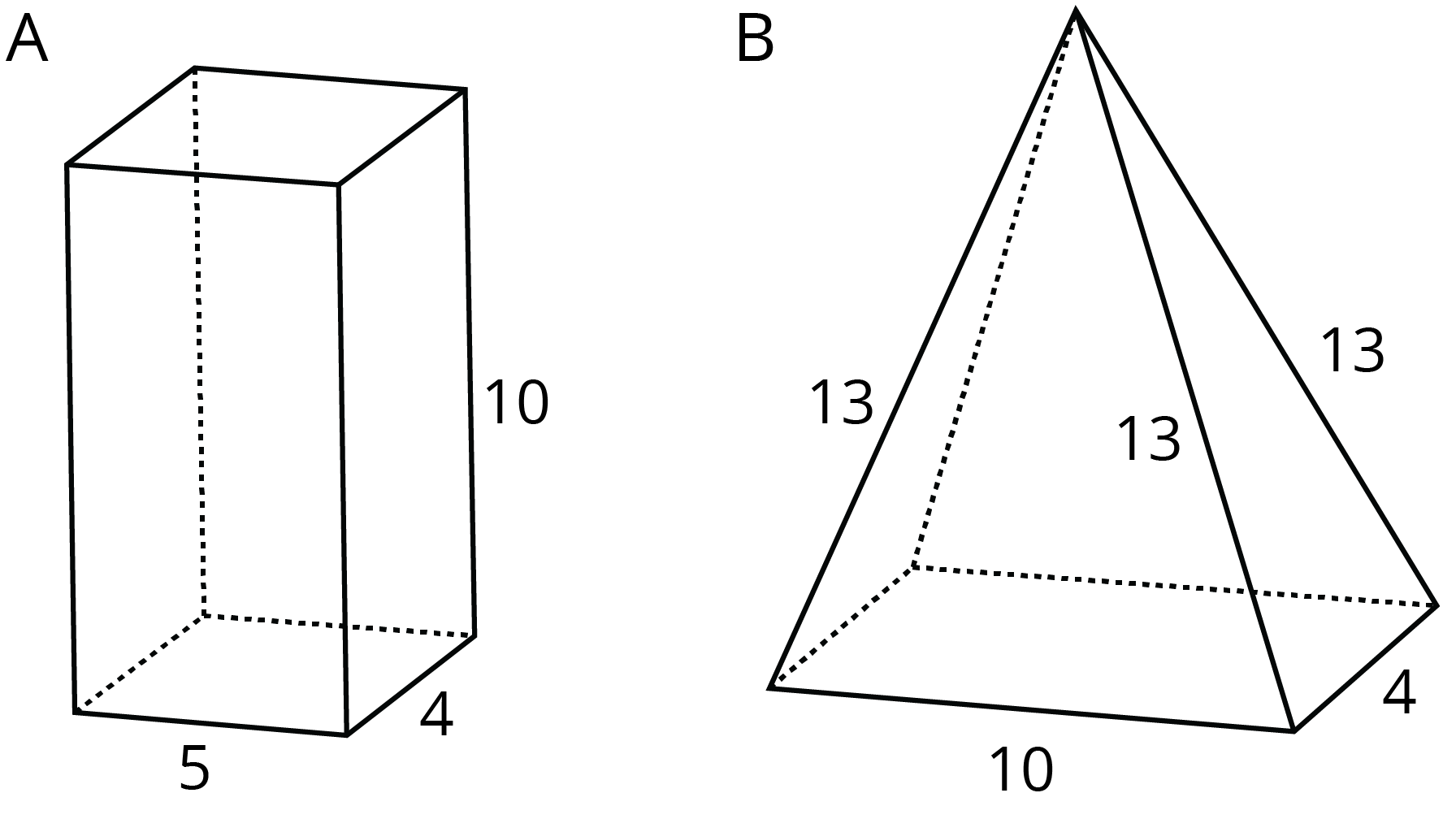
Here are two polyhedra and their nets. Label all edges in the net with the correct lengths.

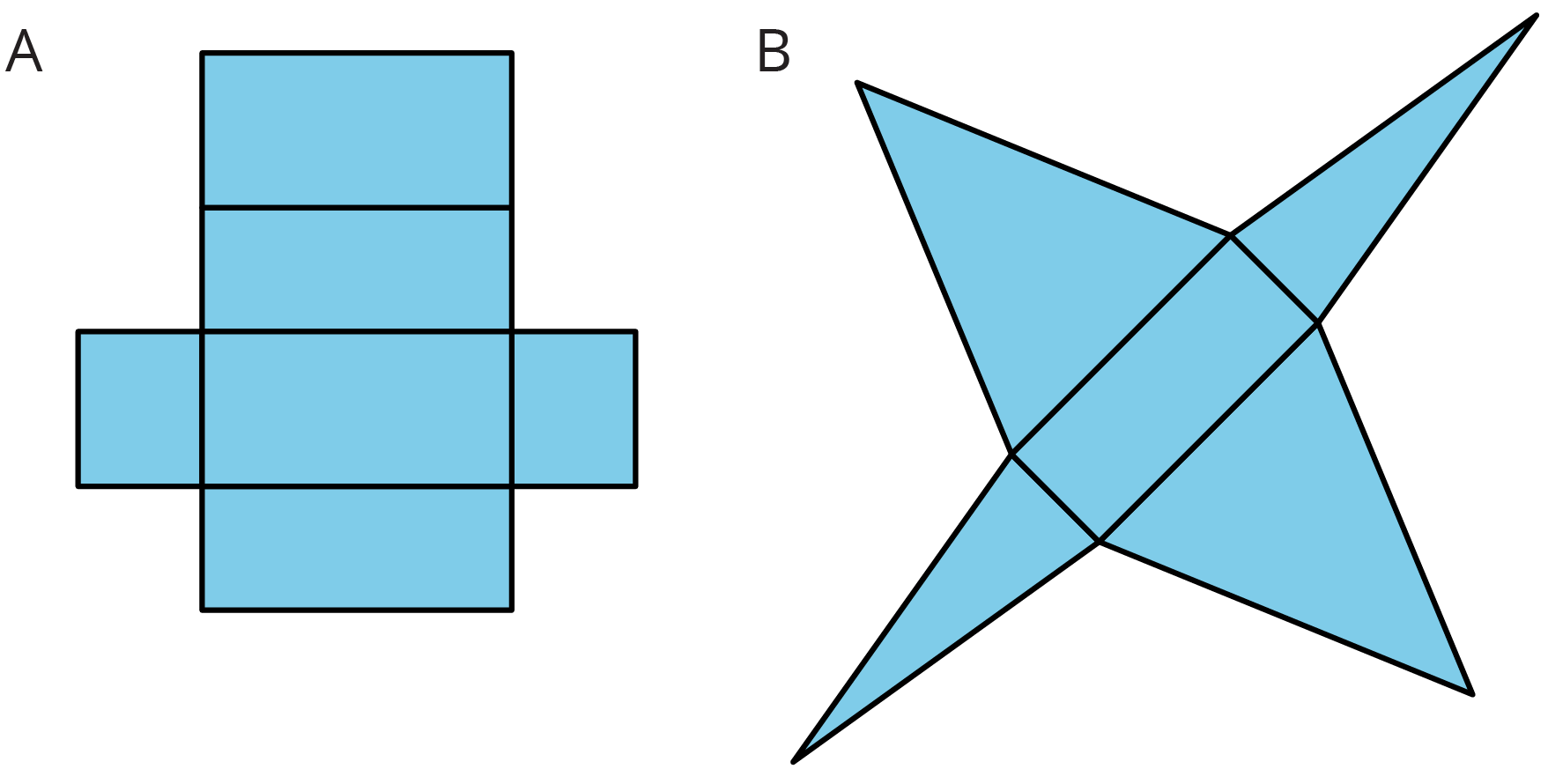
Two polyhedra labeled A and B. Polyhedron A has sides labeled 5, 4, and 10. Polyhedron B has sides labeled 4, 10, 13, 13, and 13.

Problem 5 (from Unit 1, Lesson 14)

  1. What three-dimensional figure can be assembled from the net?
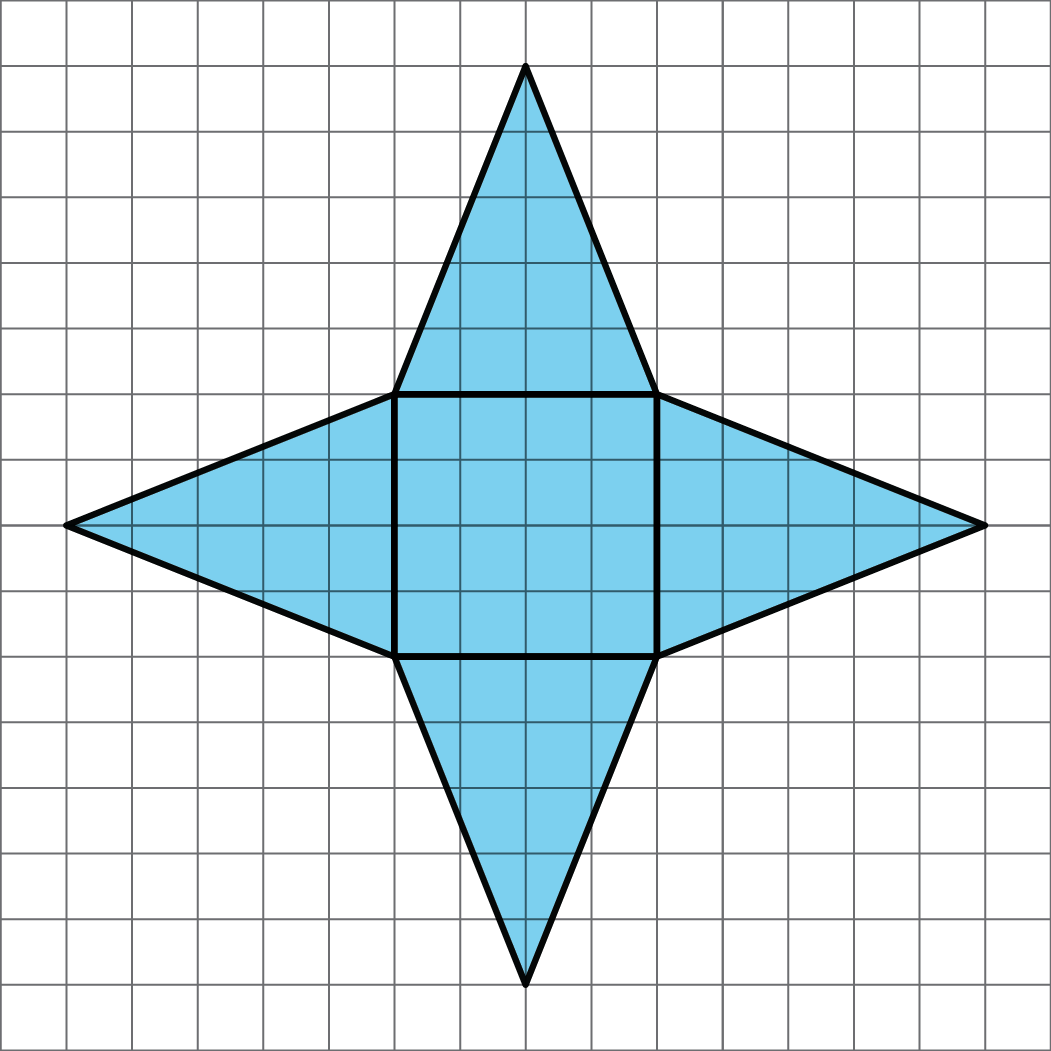
  1. What is the surface area of the figure? (One grid square is 1 square unit.)

Lesson 16

Problem 1

Match each quantity with an appropriate unit of measurement.

  1. The surface area of a tissue box
  2. The amount of soil in a planter box
  3. The area of a parking lot
  4. The length of a soccer field
  5. The volume of a fish tank
  1. Square meters
  2. Yards
  3. Cubic inches
  4. Cubic feet
  5. Square centimeters

Problem 2

Here is a figure built from snap cubes.

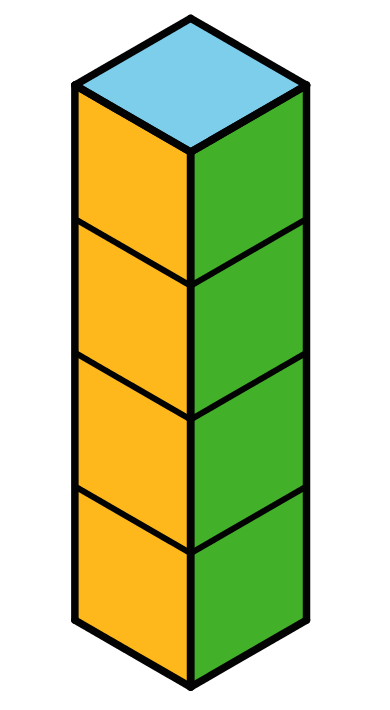
  1. Find the volume of the figure in cubic units.
  2. Find the surface area of the figure in square units.
  1. True or false: If we double the number of cubes being stacked, both the volume and surface area will double. Explain or show how you know.

Problem 3

Lin said, “Two figures with the same volume also have the same surface area.”

  1. Which two figures suggest that her statement is true?
  2. Which two figures could show that her statement is not true?

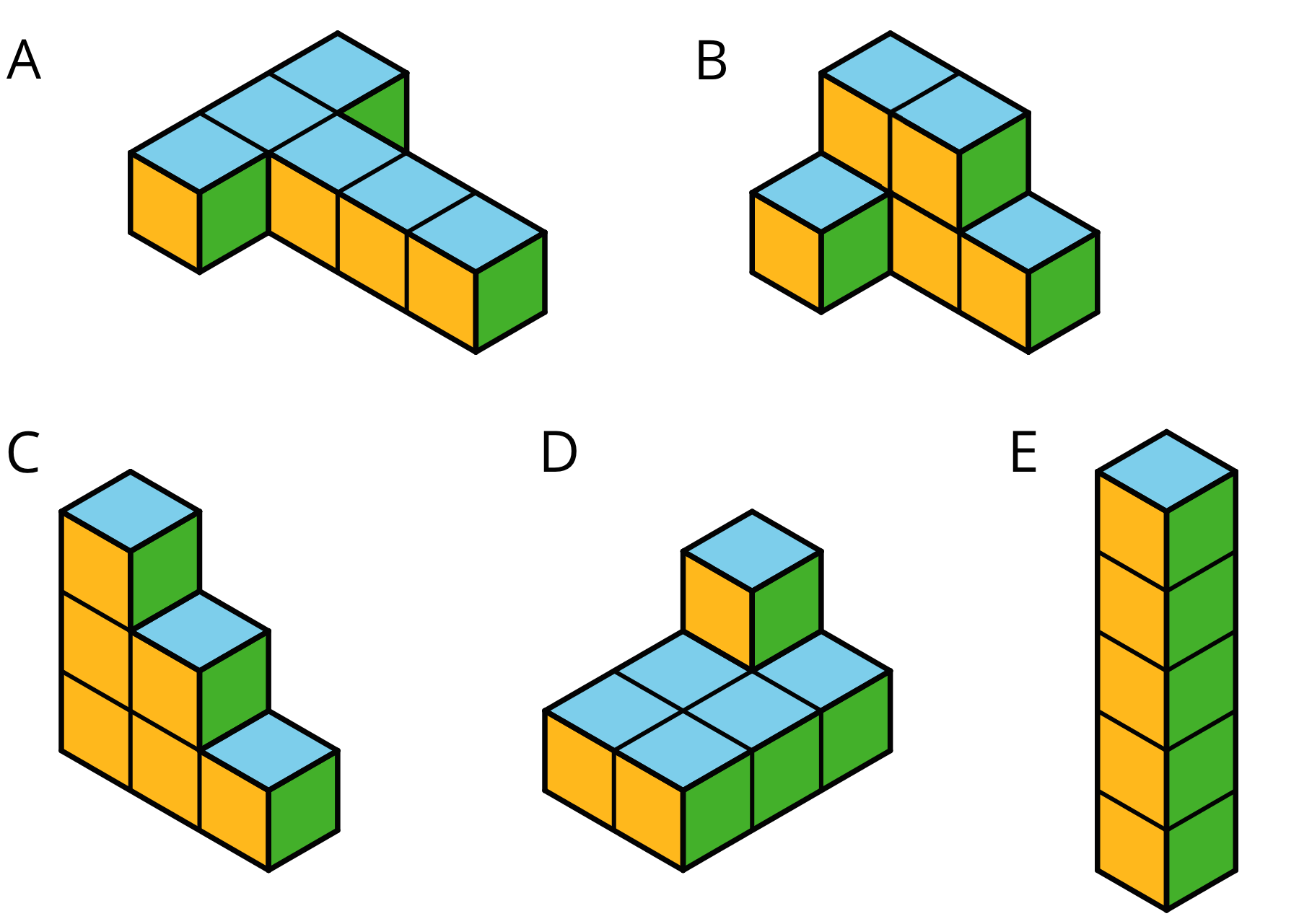
Problem 4 (from Unit 1, Lesson 11)

Draw a pentagon (five-sided polygon) that has an area of 32 square units. Label all relevant sides or segments with their measurements, and show that the area is 32 square units.

Problem 5 (from Unit 1, Lesson 15)

  1. Draw a net for this rectangular prism.
  2. Find the surface area of the rectangular prism.

Lesson 17

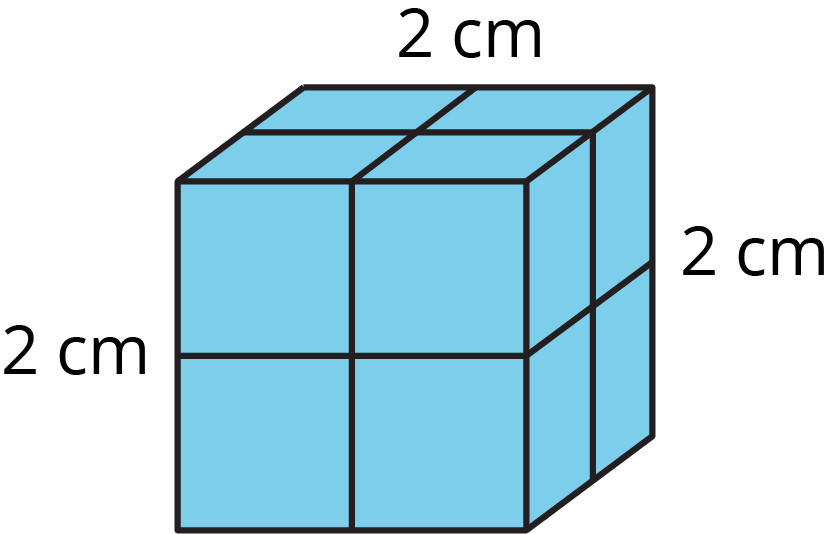
Problem 1

What is the volume of this cube?

Problem 2

a. Decide if each number on the list is a perfect square.

  1. 16
  2. 20
  3. 25
  4. 100
  1. 125
  2. 144
  3. 225
  4. 10,000

b. Write a sentence that explains your reasoning.

Problem 3

  1. Decide if each number on the list is a perfect cube.

    1. 1
    2. 3
    3. 8
    4. 9
    1. 27
    2. 64
    3. 100
    4. 125

    b. Explain what a perfect cube is.

Problem 4

  1. A square has side length 4 cm. What is its area?

  2. The area of a square is 49 m2. What is its side length?

  3. A cube has edge length 3 in. What is its volume?

Problem 5 (from Unit 1, Lesson 16)

Prism A and Prism B are rectangular prisms. Prism A is 3 inches by 2 inches by 1 inch. Prism B is 1 inch by 1 inch by 6 inches.

Select all statements that are true about the two prisms.

  1. They have the same volume.
  2. They have the same number of faces.
  3. More inch cubes can be packed into Prism A than into Prism B.
  4. The two prisms have the same surface area.
  5. The surface area of Prism B is greater than that of Prism A.

Problem 6 (from Unit 1, Lesson 14)

  1. What polyhedron can be assembled from this net?
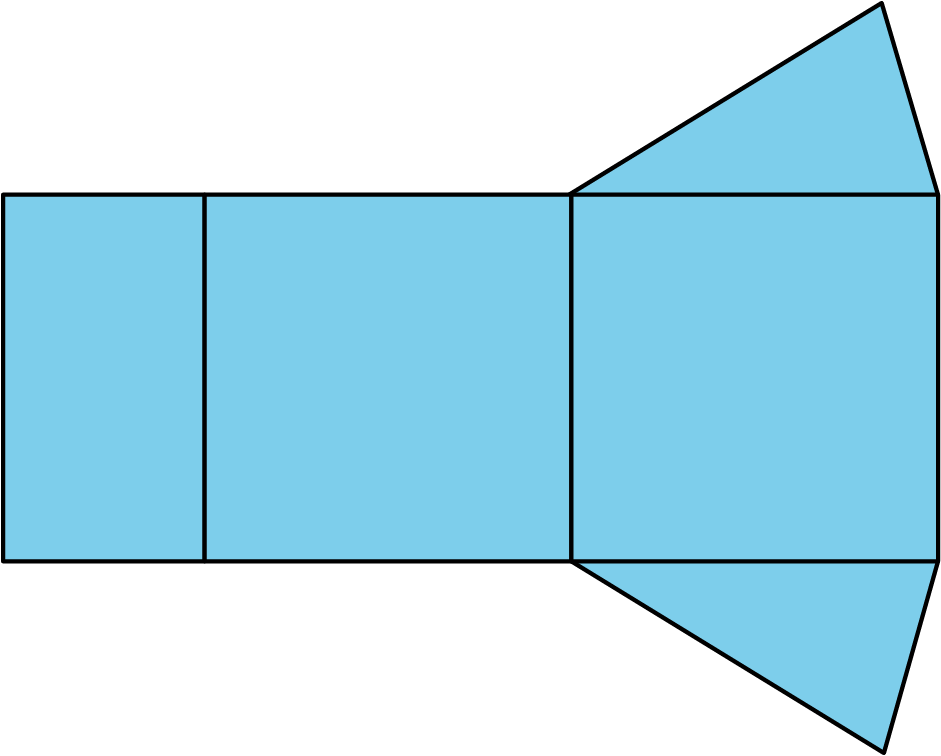
  1. What information would you need to find its surface area? Be specific, and label the diagram as needed.

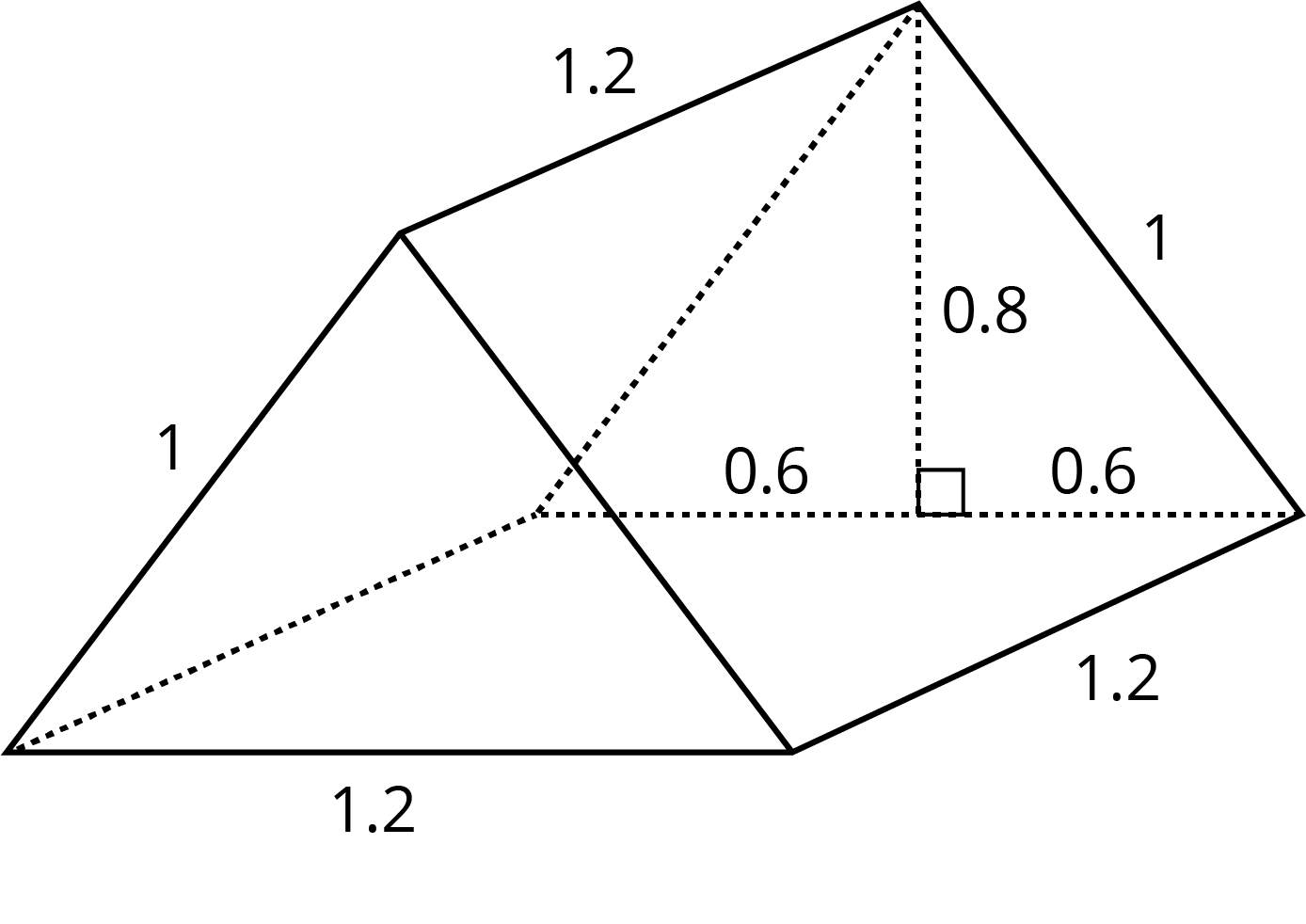
Problem 7 (from Unit 1, Lesson 15)

Find the surface area of this triangular prism. All measurements are in meters.

Lesson 18

Problem 1

  1. What is the volume of a cube with edge length 8 in?

  2. What is the volume of a cube with edge length $\frac 13$ cm?

  3. A cube has a volume of 8 ft3. What is its edge length?

Problem 2

a. What three-dimensional figure can be assembled from this net?

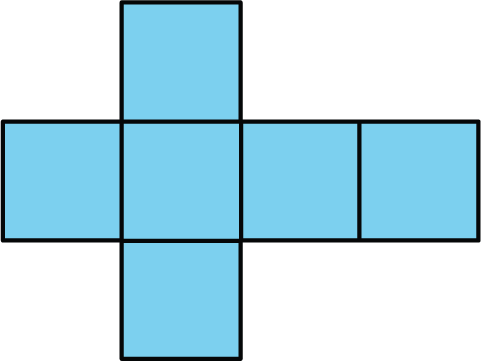
b. If each square has a side length of 61 cm, write an expression for the surface area and another for the volume of the figure.

Problem 3

  1. Draw a net for a cube with edge length $x$ cm.

  2. What is the surface area of this cube?

  3. What is the volume of this cube?

Problem 4 (from Unit 1, Lesson 14)

Here is a net for a rectangular prism that was not drawn accurately. 

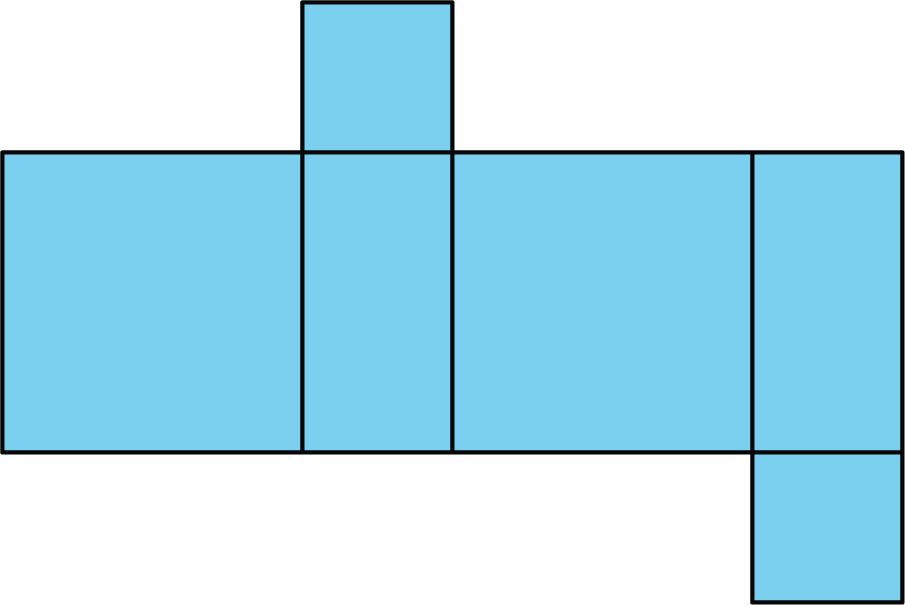
  1. Explain what is wrong with the net.
  2. Draw a net that can be assembled into a rectangular prism.
  3. Create another net for the same prism.
 

Problem 5 (from Unit 1, Lesson 13)

State whether each figure is a polyhedron. Explain how you know.

Problem 6 (from Unit 1, Lesson 12)

Here is Elena’s work for finding the surface area of a rectangular prism that is 1 foot by 1 foot by 2 feet.

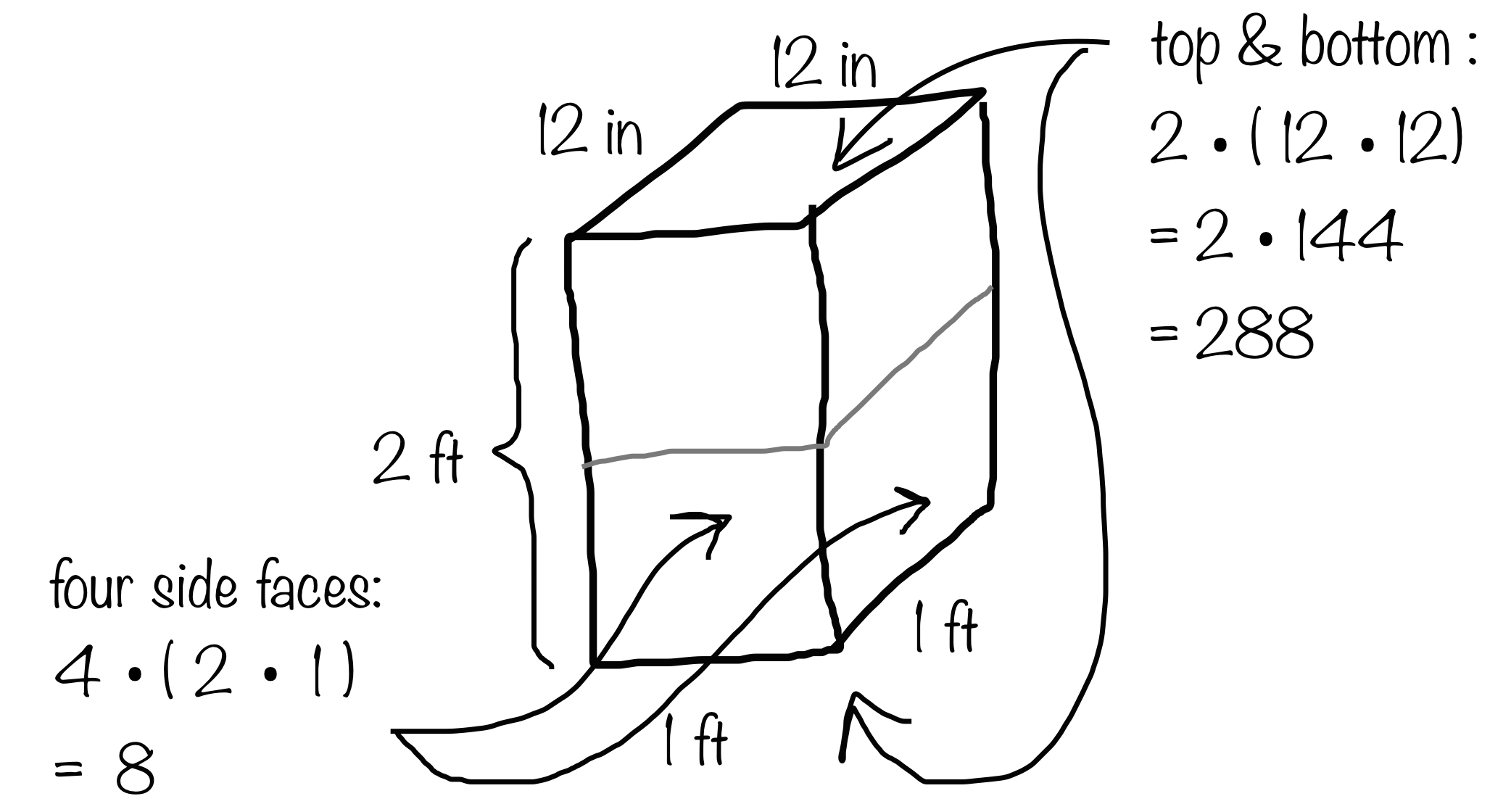
She concluded that the surface area of the prism is 296 square feet. Do you agree with her conclusion? Explain your reasoning.

Lesson 19

No practice problems for this lesson.