Let’s solve percentage problems like a pro.
Find the value of each expression mentally.
$(0.23) \boldcdot 100$
$50 \div 100$
$145 \boldcdot \frac{1}{100}$
$7 \div 100$
A school held several evening activities last month—a music concert, a basketball game, a drama play, and literacy night. The music concert was attended by 250 people. How many people came to each of the other activities?
50% of the people who attended the drama play also attended the music concert. What percentage of the people who attended the music concert also attended the drama play?
During a sale, every item in a store is 80% of its regular price.
| item 1 | item 2 | item 3 | item 4 | item 5 | ||
|---|---|---|---|---|---|---|
| row 1 | regular price | \$1 | \$4 | \$10 | \$55 | \$120 |
| row 2 | sale price |
You found 80% of many values. Was there a process you repeated over and over to find the sale prices? If so, describe it.
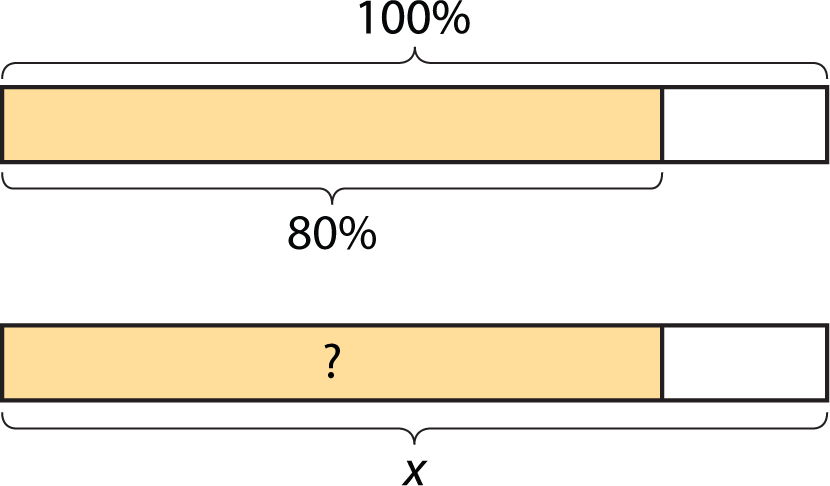
Which of the following expressions could be used to find 80% of $x$? Be prepared to explain your reasoning.
$\frac{8}{100} \boldcdot x$
$\frac{80}{100} \boldcdot x$
$\frac{8}{10} \boldcdot x$
$\frac{4}{10} \boldcdot x$
$\frac85 \boldcdot x$
$\frac45 \boldcdot x$
$80 \boldcdot x$
$8 \boldcdot x$
$(0.8) \boldcdot x$
$(0.08) \boldcdot x$
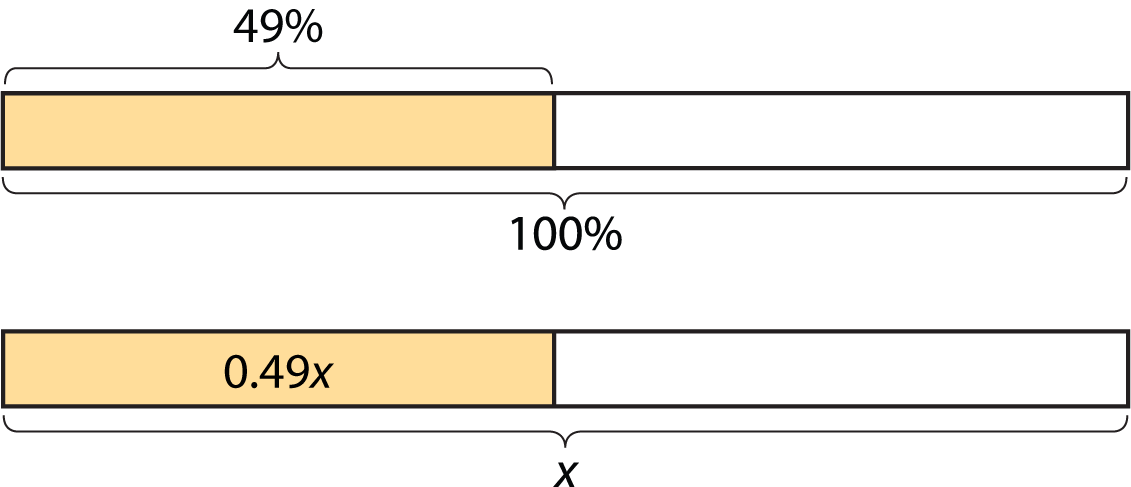
To find 49% of a number, we can multiply the number by $\frac{49}{100}$ or 0.49.
To find 135% of a number, we can multiply the number by $\frac{135}{100}$ or 1.35.
To find 6% of a number, we can multiply the number by $\frac{6}{100}$ or 0.06.
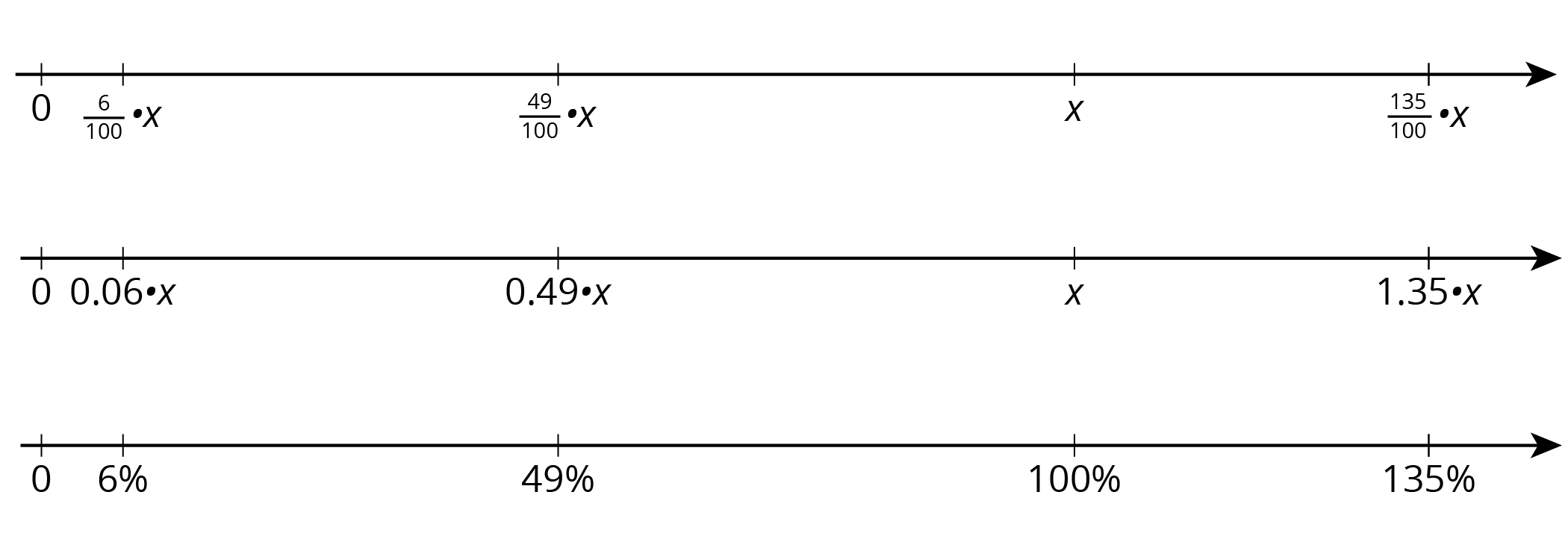
In general, to find $P\%$ of $x$, we can multiply: $$\frac{P}{100} \boldcdot x$$
