Lesson 13: The Median of a Data Set

Let's explore the median of a data set and what it tells us.

13.1: The Plot of the Story

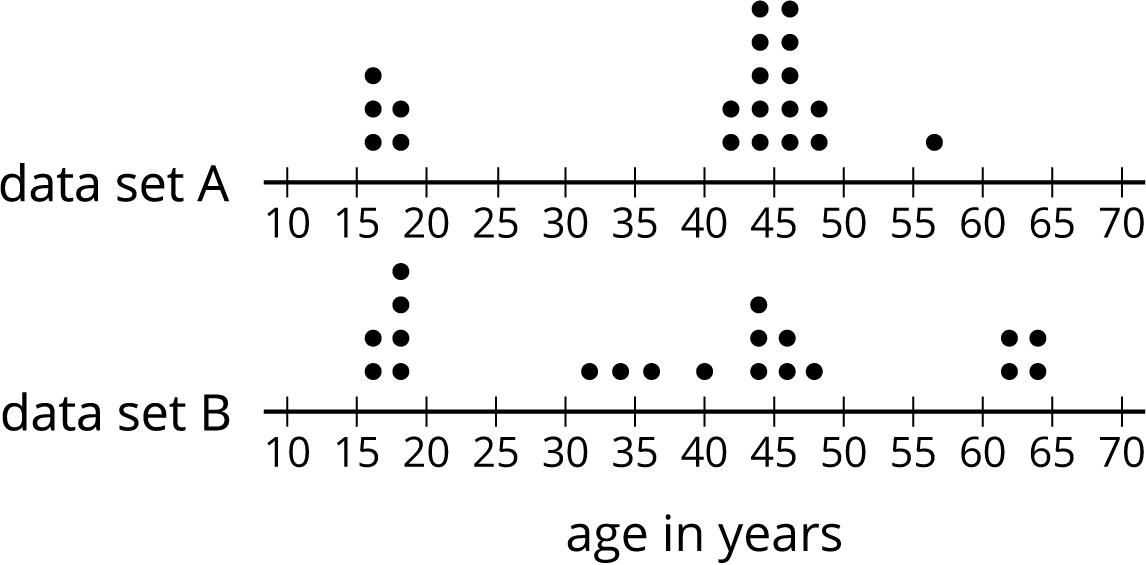
  1. Here are two dot plots and two stories. Match each story with a dot plot that could represent it. Be prepared to explain your reasoning.

    Two dot plots for "age in years" labeled "data set A" and "data set B." For each dot plot, the numbers 10 through 70, in increments of 5, are indicated. The approximate data for “data set A” are as follows: 16 years, 3 dots; 18 years, 2 dots; 42 years, 2 dots; 44 years, 5 dots; 46 years, 5 dots; 48 years, 2 dots; 56 years, 1 dot. The approximate data for “data set B” are as follows: 16 years, 2 dots; 18 years, 4 dots; 32 years, 1 dot; 34 years, 1 dot; 36 years, 1 dot; 40 years, 1 dot; 44 years, 3 dots; 46 years, 2 dots; 48 years, 1 dot; 62 years, 2 dots; 64 years, 2 dots.
     

    • Twenty people—high school students, parents, guardians, and teachers—attended a rehearsal for a high school musical. The mean age was 38.5 years and the MAD was 16.5 years.

    • High school soccer team practice is usually watched by family members of the players. One evening, twenty people watched the team practice. The mean age was 38.5 years and the MAD was 12.7 years.
  2. Another evening, twenty people watched the soccer team practice. The mean age was similar to that from the first evening, but the MAD was greater (about 20 years).

    Make a dot plot that could illustrate the distribution of ages in this story.

    A blank dot plot for “age in years.” The numbers 10 through 70, in increments of 5, are indicated.

13.2: Siblings in the House

Here is a table that shows the numbers of siblings of ten students in Tyler’s class.

1 0 2 1 7 0 2 0 1 10
  1. Represent the data shown in the table with a dot plot.

  2. Based on your dot plot, estimate the center of the data without making any calculations. What is your estimate of a typical number of siblings of these sixth-grade students? Mark the location of that number on your dot plot.

  3. Find the mean. Show your reasoning.
    1. How does the mean compare to the value that you marked on the dot plot as a typical number of siblings? (Is the mean that you calculated a little larger, a lot larger, exactly the same, a little smaller, or a lot smaller than your estimate?)
    2. Do you think the mean summarizes the data set well? Explain your reasoning.

13.3: Finding the Middle

  1. Your teacher will give you an index card. Write your first and last names on the card. Then record the total number of letters in your name. After that, pause for additional instructions from your teacher.

    1. Here is the data set on numbers of siblings from an earlier activity. Sort the data from least to greatest, and then find the median.
      row 1 1 0 2 1 7 0 2 0 1 10
    2. In this situation, do you think the median is a good measure of a typical number of siblings for this group? Explain your reasoning.
    1. Here is the dot plot showing the travel time, in minutes, of Elena’s bus rides to school. Find the median travel time. Be prepared to explain your reasoning.
      A dot plot labeled “travel time in minutes.” The numbers 5 through 14 are indicated. The data is as follows. 5 minutes, 0 dots 6 minutes, 2 dots 7 minutes, 1 dot 8 minutes, 3 dots 9 minutes, 3 dots 10 minutes, 2 dots 11 minutes, 0 dots 12 minutes, 1 dot 13 minutes, 0 dots 14 minutes, 0 dots
    2. What does the median tell us in this context?

Summary

The median is another measure of center of a distribution. It is the middle value in a data set when values are listed in order. Half of the values in a data set are less than or equal to the median, and half of the values are greater than or equal to the median.

To find the median, we order the data values from least to greatest and find the number in the middle.

Suppose we have 5 dogs whose weights, in pounds, are shown in the table. The median weight for this group of dogs is 32 pounds because three dogs weigh less than or equal to 32 pounds and three dogs weigh greater than or equal to 32 pounds.

20 25 32 40 55

Now suppose we have 6 cats whose weights, in pounds, are as shown in the table. Notice that there are two values in the middle: 7 and 8.

4 6 7 8 10 10

The median weight must be between 7 and 8 pounds, because half of the cats weigh less or equal to 7 pounds and half of the cats weigh greater than or equal to 8 pounds.

In general, when we have an even number of values, we take the number exactly in between the two middle values. In this case, the median cat weight is 7.5 pounds because $(7+8)\div 2=7.5$.

Practice Problems ▶

Glossary

median

median

The median of a data set is the middle value when the data values are listed in order. If the number of values is even, it is the mean of the two middle values.