8.1: Number Talk: Remainders in Division
Find the quotient mentally.
246\div 12
Let’s use ratios to describe how much things cost.
Find the quotient mentally.
246\div 12
Eight avocados cost $4.
Twelve large bottles of water cost $9.
A 10-pound sack of flour costs $8.
Here is an applet you can use if you choose to.
Is bigger always better? It is commonly thought that buying larger packages or containers, sometimes called buying in bulk, is a great way to save money. For example, a 6-pack of soda might cost $3 while a 12-pack of the same brand costs $5.
Find 3 different cases where it is not true that buying in bulk saves money. You may use the internet or go to a local grocery store and take photographs of the cases you find. Make sure the products are the same brand. For each example that you find, give the quantity or size of each, and describe how you know that the larger size is not a better deal.
Four bags of chips cost $6.
What is the cost per bag?
At this rate, how much will 7 bags of chips cost?
What is the cost per book?
At this rate, how many books can you buy for $21?
What is the cost per bracelet?
At this rate, how much will 11 neon bracelets cost?
Pause here so your teacher can review your work. Next, your teacher will assign you one of the problems.
Create a visual display that shows your solution to your assigned problem. Be prepared to share your solution with the class.
Here is an applet you may use if you choose to.
The unit price is the price of 1 thing—for example, the price of 1 ticket, 1 slice of pizza, or 1 kilogram of peaches.
If 4 movie tickets cost $28, then the unit price would be the cost per ticket. We can create a double number line to find the unit price.
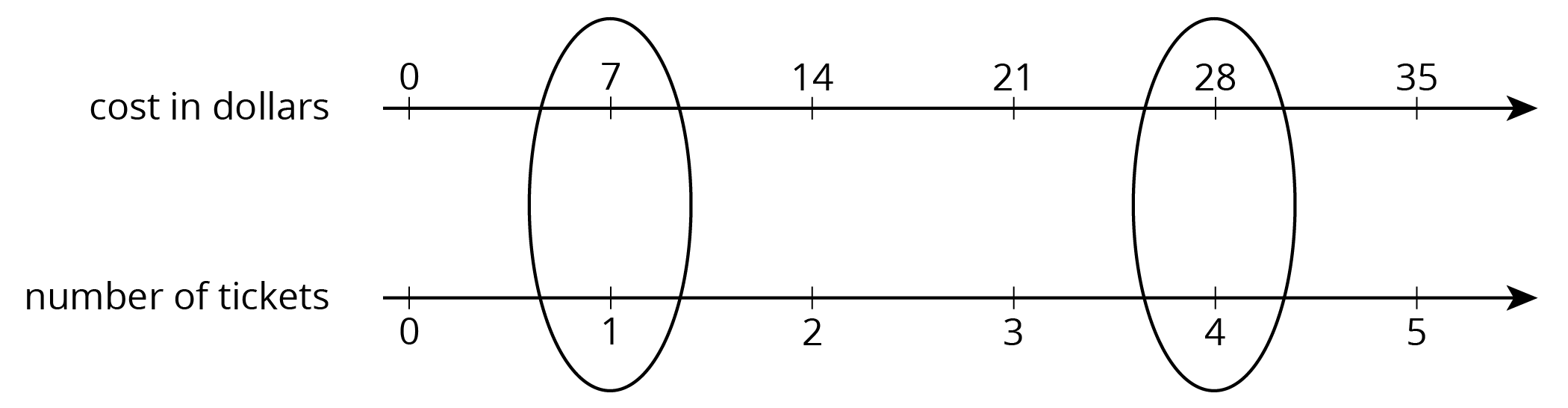
This double number line shows that the cost for 1 ticket is $7. We can also find the unit price by dividing, 28 \div 4 = 7, or by multiplying, 28 \boldcdot \frac14 = 7.
The unit price is the cost for one item or one unit of measure.