Lesson 3: Interpreting Division Situations

Let’s explore situations that involve division.

3.1: Dot Image: Properties of Multiplication

An arrangement of dots.

3.2: Homemade Jams

Draw a diagram and write a multiplication equation to represent each of the following situations. Then answer the question.

  1. Mai had 4 jars. In each jar, she put $2\frac14$ cups of homemade blueberry jam. Altogether, how many cups of jam are in the jars?
  2. Priya filled 5 jars, using a total of $7\frac12$ cups of strawberry jam. How many cups of jam are in each jar?
  3. Han had some jars. He put $\frac34$ cup of grape jam in each jar, using a total of $6\frac34$ cups. How many jars did he fill?

Here is an applet to use if you choose to.

The toolbar includes buttons that represent 1 whole and fractional parts, as shown here. Click a button to choose a quantity, and then click in the work space of the applet window to drop it. When you're done choosing pieces, use the Move tool (the arrow) to drag them into the jars. You can always go back and get more pieces, or delete them with the Trash Can tool.

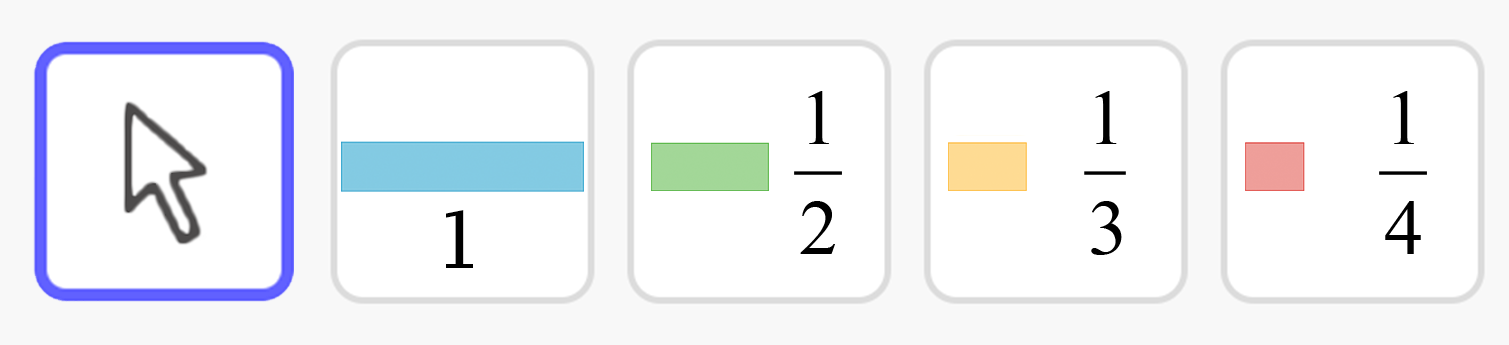
The jars in this applet are shown as stacked to make it easier to combine the jam and find out how much you have.

GeoGebra Applet A659cMp3

Here are the questions again.

  1. Mai had 4 jars. In each jar, she put $2\frac14$ cups of homemade blueberry jam. Altogether, how many cups of jam are in the jars?
  2. Priya filled 5 jars, using a total of $7\frac12$ cups of strawberry jam. How many cups of jam are in each jar?
  3. Han had some jars. He put $\frac34$ cup of grape jam in each jar, using a total of $6\frac34$ cups. How many jars did he fill?

3.3: Making Granola

  1. To make 1 batch of granola, Kiran needs 26 ounces of oats. The only measuring tool he has is a 4-ounce scoop. How many scoops will it take to measure 26 ounces of oats?

    1. Will the answer be more than 1 or less than 1?
    2. Write a multiplication equation and a division equation that represent this situation. Use “?” to represent the unknown quantity.
    3. Find the unknown quantity. If you get stuck, draw a diagram.

  2. The recipe calls for 14 ounces of mixed nuts. To get that amount, Kiran uses 4 bags of mixed nuts.

    1. Write a mathematical question that might be asked about this situation.
    2. What might the equation $14 \div 4 =\, {?}$ represent in Kiran’s situation?
    3. Find the quotient. Show your reasoning. If you get stuck, draw a diagram.

Summary

If a situation involves equal-sized groups, it is helpful to make sense of it in terms of the number of groups, the size of each group, and the total amount. Here are three examples to help us better understand such situations.

  • Suppose we have 3 bottles with $6\frac12$ ounces of water in each, and the total amount of water is not given. Here we have 3 groups, $6\frac12$ ounces in each group, and an unknown total, as shown in this diagram:

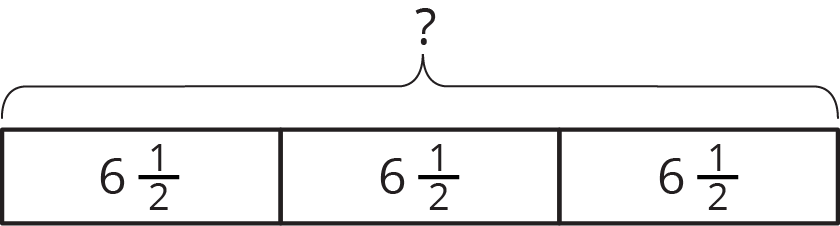
    A tape diagram of 3 equal parts. Each part is labeled six and one half. A brace from the beginning of the diagram to the end of the disgram is labeled with a question mark.

    We can express this situation as a multiplication problem. The unknown is the product, so we can simply multiply the 2 known numbers to find it. $$3 \boldcdot  6\frac12 = {?}$$

  • Next, suppose we have 20 ounces of water to fill 6 equal-sized bottles, and the amount in each bottle is not given. Here we have 6 groups, an unknown amount in each, and a total of 20. We can represent it like this:

    A tape diagram of 6 equal parts. Each part is labeled with a question mark. A brace from the beginning of the diagram to the end of the diagram is labeled with 20.

    This situation can also be expressed using multiplication, but the unknown is a factor, rather than the product: $$6\, \boldcdot {?} = 20$$

    To find the unknown, we cannot simply multiply, but we can think of it as a division problem: $$20 \div 6 = \,?$$

  • Now, suppose we have 40 ounces of water to pour into bottles, 12 ounces in each bottle, but the number of bottles is not given. Here we have an unknown number of groups, 12 in each group, and a total of 40.

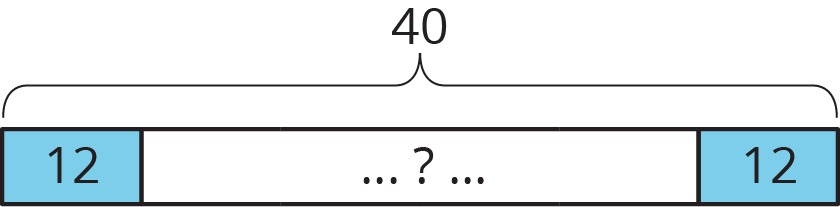
    A tape diagram with 3 parts. The first part and third part are equal and are labeled 12. The second part is labeled with a question mark. A brace from the beginning of the diagram to the end of the diagram is labeled 40.

    Again, we can think of this in terms of multiplication, with a different factor being the unknown: $$? \boldcdot 12 = 40$$

    Likewise, we can use division to find the unknown: $$40 \div 12 = \,?$$

Whenever we have a multiplication situation, one factor tells us how many groups there are, and the other factor tells us how much is in each group.

Sometimes we want to find the total. Sometimes we want to find how many groups there are. Sometimes we want to find how much is in each group. Anytime we want to find out how many groups there are or how much is in each group, we can represent the situation using division.

Practice Problems ▶