Lesson 9: Constant Speed

Let’s use ratios to work with how fast things move.

9.1: Number Talk: Dividing by Powers of 10

Find the quotient mentally.

$30\div 10$

$34\div 10$

$3.4\div 10$

$34\div 100$

9.2: Moving 10 Meters

Your teacher will set up a straight path with a 1-meter warm-up zone and a 10-meter measuring zone. Follow the following instructions to collect the data.

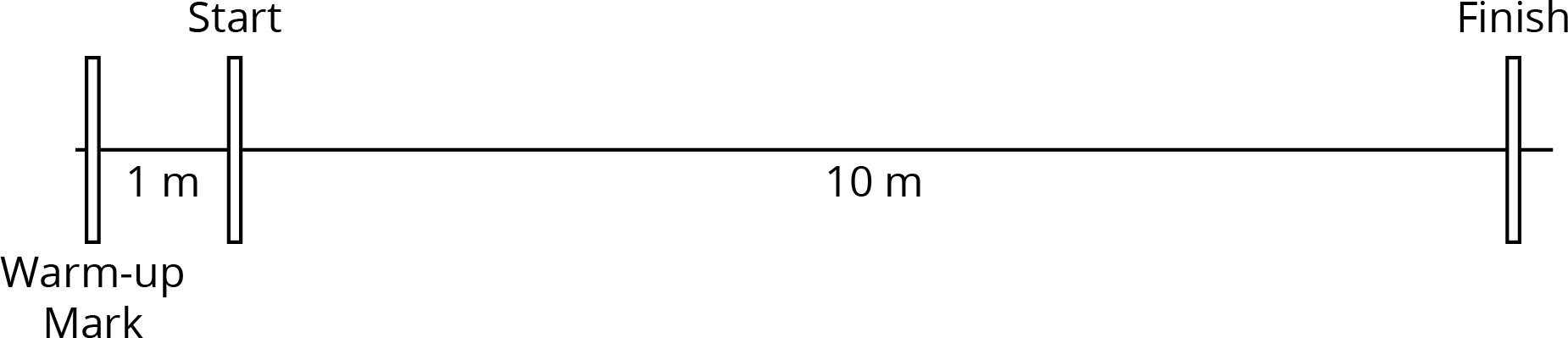
​A diagram of a line with three markings. The first mark is labeled "Warm-up Mark", the second mark is labeled "Start", and the third mark is labeled "Finish". The distance between the first and second mark is labeled 1m. The distance between the second and third mark is labeled 10m.
    1. The person with the stopwatch (the “timer”) stands at the finish line. The person being timed (the “mover”) stands at the warm-up line.
    2. On the first round, the mover starts moving at a slow, steady speed along the path. When the mover reaches the start line, they say, “Start!” and the timer starts the stopwatch.
    3. The mover keeps moving steadily along the path. When they reach the finish line, the timer stops the stopwatch and records the time, rounded to the nearest second, in the table.
    4. On the second round, the mover follows the same instructions, but this time, moving at a quick, steady speed. The timer records the time the same way.
    5. Repeat these steps until each person in the group has gone twice: once at a slow, steady speed, and once at a quick, steady speed.
        your slow moving time (seconds) your fast moving time (seconds)
      row 1    

  2. After you finish collecting the data, use the double number line diagrams to answer the questions. Use the times your partner collected while you were moving.

    Moving slowly:

    A double number line with 2 tick marks is titled "Moving slowly." The top number line is labeled "distance traveled, in meters" and the numbers 0 and 10 are indicated. The bottom number line is labeled "elasped time, in seconds". The number 0 is at the first tick mark and the second tick mark is blank.

    Moving quickly:

    A double number line for meters of distance traveled: 0, 10 and seconds of elapsed time: 0, blank.
    1. Estimate the distance in meters you traveled in 1 second when moving slowly.
    2. Estimate the distance in meters you traveled in 1 second when moving quickly.
    3. Trade diagrams with someone who is not your partner. How is the diagram representing someone moving slowly different from the diagram representing someone moving quickly?

9.3: Moving for 10 Seconds

Lin and Diego both ran for 10 seconds, each at a constant speed. Lin ran 40 meters and Diego ran 55 meters. 

  1. Who was moving faster? Explain how you know.
  2. How far did each person move in 1 second? If you get stuck, consider drawing double number line diagrams to represent the situations.
  3. Use your data from the previous activity. How far could you travel in 10 seconds at your quicker speed?
  4. Han ran 100 meters in 20 seconds at a constant speed. Is this speed faster, slower, or the same as Lin’s? Diego’s? Yours?

GeoGebra Applet ycJSQpXT

GeoGebra Applet ycJSQpXT

Summary

Suppose a train traveled 100 meters in 5 seconds at a constant speed. To find its speed in meters per second, we can create a double number line:

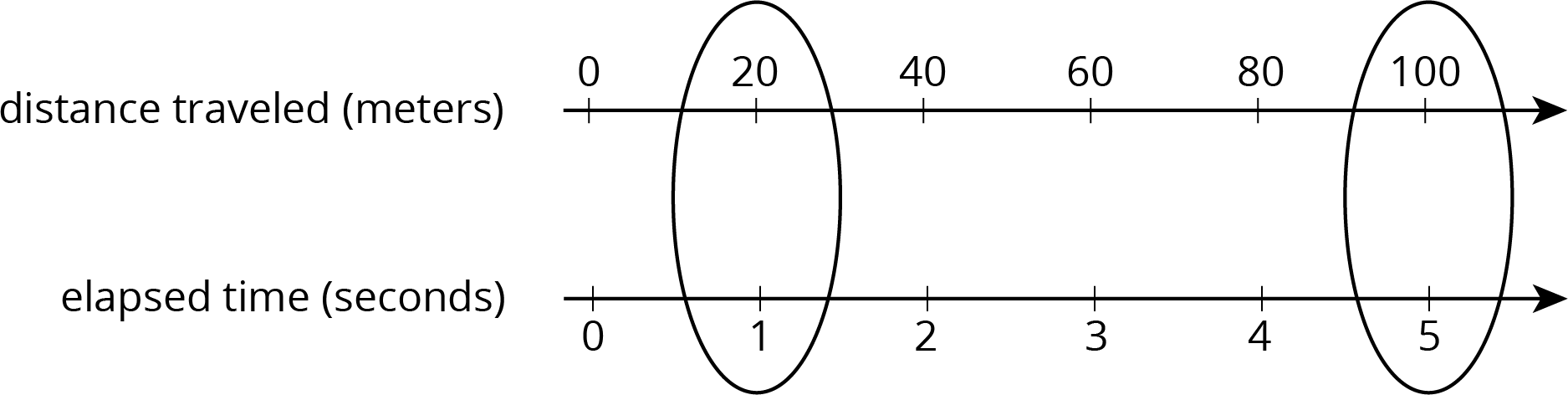
A double number line for meters of distance traveled: 0, 20, 40, 60, 80, 100 and seconds of elapsed time: 0, 1, 2, 3, 4, 5.

The double number line shows that the train’s speed was 20 meters per second. We can also find the speed by dividing: $100 \div 5 = 20$.

Once we know the speed in meters per second, many questions about the situation become simpler to answer because we can multiply the amount of time an object travels by the speed to get the distance. For example, at this rate, how far would the train go in 30 seconds? Since $20 \boldcdot 30 = 600$, the train would go 600 meters in 30 seconds.

Practice Problems ▶

Glossary

meters per second

meters per second

A unit to measure speed that tells you how many meters an object travels in one second.