- Draw a tape diagram to represent the equation.
Unit 6: Practice Problem Sets
Lesson 1
Problem 1
Here is an equation: $x + 4 = 17$
- Which part of the diagram shows the quantity $x$? What about 4? What about 17?
- How does the diagram show that $x+4$ has the same value as 17?
Problem 2
Diego is trying to find the value of $x$ in $5 \boldcdot x = 35$. He draws this diagram but is not certain how to proceed.

- Complete the tape diagram so it represents the equation $5 \boldcdot x = 35$.
- Find the value of $x$.
Problem 3
For each equation, draw a tape diagram and find the unknown value.
- $x+9=16$
- $4 \boldcdot x = 28$
Problem 4
Match each equation to one of the two tape diagrams.

- $x + 3 = 9$
- $3 \boldcdot x = 9$
- $9=3 \boldcdot x$
- $3+x=9$
- $x = 9 - 3$
- $x = 9 \div 3$
- $x + x+ x = 9$
Problem 5 (from Unit 5, Lesson 13)
A shopper paid \$2.52 for 4.5 pounds of potatoes, \$7.75 for 2.5 pounds of broccoli, and \$2.45 for 2.5 pounds of pears. What is the unit price of each item she bought? Show your reasoning.
Problem 6 (from Unit 3, Lesson 14)
A sports drink bottle contains 16.9 fluid ounces. Andre drank 80% of the bottle. How many fluid ounces did Andre drink? Show your reasoning.
Problem 7 (from Unit 3, Lesson 11)
The daily recommended allowance of calcium for a sixth grader is 1,200 mg. One cup of milk has 25% of the recommended daily allowance of calcium. How many milligrams of calcium are in a cup of milk? If you get stuck, consider using the double number line.

Lesson 2
Problem 1
Select all the true equations.
- $5 + 0 = 0$
- $15 \boldcdot 0 = 0$
- $1.4 + 2.7 = 4.1$
- $\frac{2}{3} \boldcdot \frac{5}{9} = \frac{7}{12}$
- $4 \frac{2}{3}=5 - \frac{1}{3}$
Problem 2
Mai's water bottle had 24 ounces in it. After she drank $x$ ounces of water, there were 10 ounces left. Select all the equations that represent this situation.
- $24 \div 10 = x$
- $24 +10 = x$
- $24 - 10 = x$
- $x + 10 = 24$
- $10x = 24$
Problem 3
Priya has 5 pencils, each $x$ inches in length. When she lines up the pencils end to end, they measure 34.5 inches. Select all the equations that represent this situation.
- $5 + x = 34.5$
- $5x = 34.5$
- $34.5 \div 5 = x$
- $34.5 - 5 = x$
- $x = (34.5) \boldcdot 5$
Problem 4
Match each equation with a solution from the list of values.
- $2a = 4.6$
- $b + 2 = 4.6$
- $c \div 2 = 4.6$
- $d - 2 = 4.6$
- $e+\frac{3}{8} = 2$
- $\frac{1}{8}f = 3$
- $g \div \frac{8}{5} = 1$
- $\frac{8}{5}$
- $1 \frac{5}{8}$
- 2.3
- 2.6
- 6.6
- 9.2
- 24
Problem 5 (from Unit 3, Lesson 11)
The daily recommended allowance of vitamin C for a sixth grader is 45 mg. 1 orange has about 75% of the recommended daily allowance of vitamin C. How many milligrams are in 1 orange? If you get stuck, consider using the double number line.
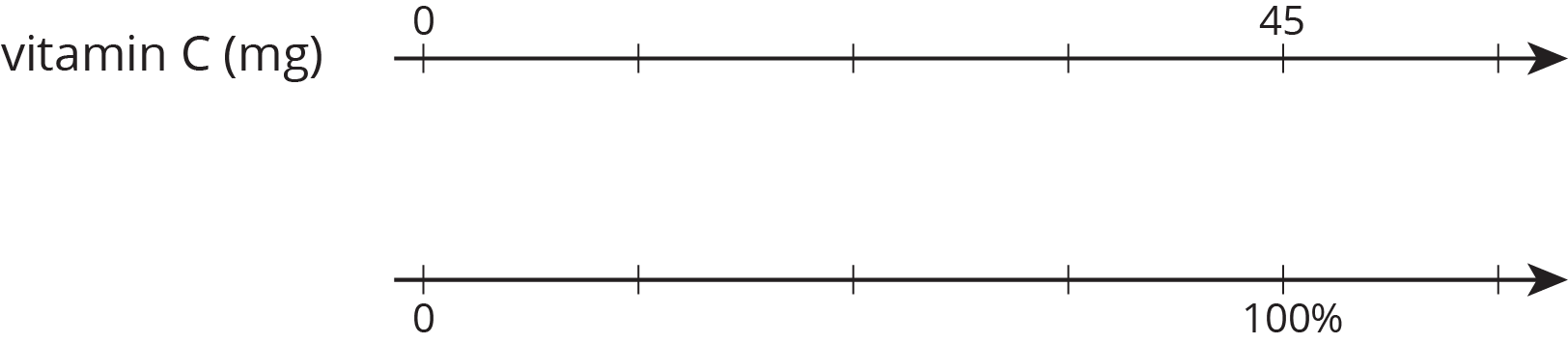
Problem 6 (from Unit 3, Lesson 12)
There are 90 kids in the band. 20% of the kids own their own instruments, and the rest rent them.
- How many kids own their own instruments?
- How many kids rent instruments?
- What percentage of kids rent their instruments?
Lesson 3
Problem 1
Select all the equations that represent the hanger.
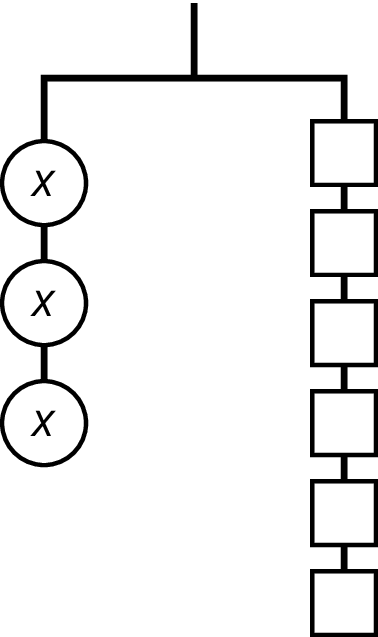
- $x+x+x = 1+1+1+1+1+1$
- $x \boldcdot x \boldcdot x = 6$
- $3x = 6$
- $x + 3 = 6$
- $x \boldcdot x \boldcdot x = 1 \boldcdot 1 \boldcdot 1 \boldcdot 1 \boldcdot 1 \boldcdot 1$
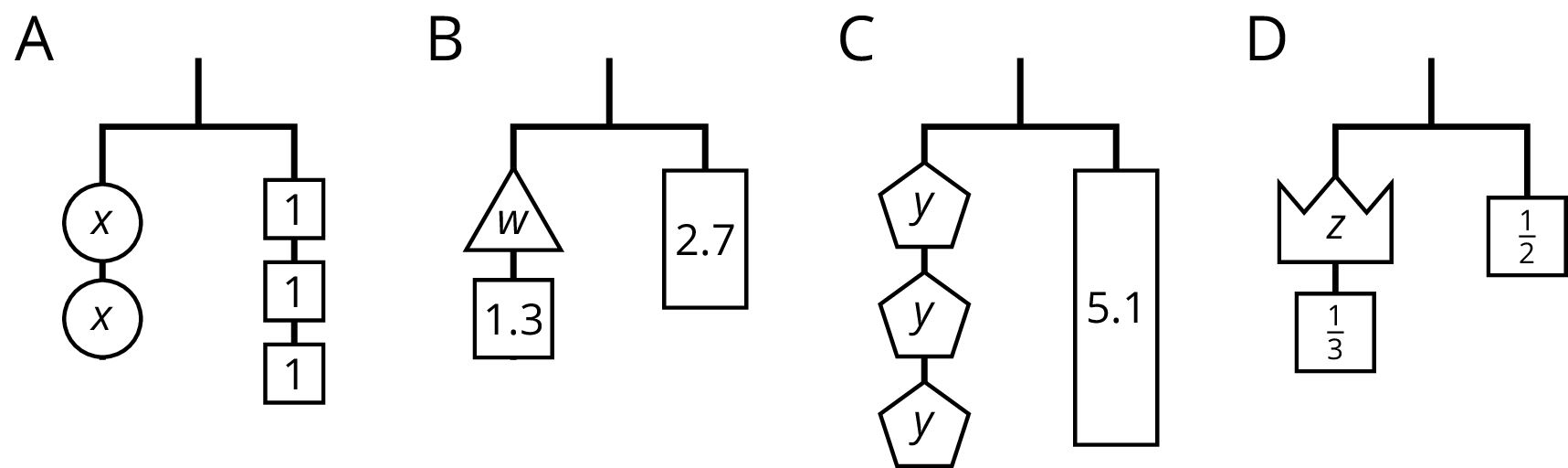
Problem 2
Write an equation to represent each hanger.
Problem 3
- Write an equation to represent the hanger.
- Explain how to reason with the hanger to find the value of $x$.
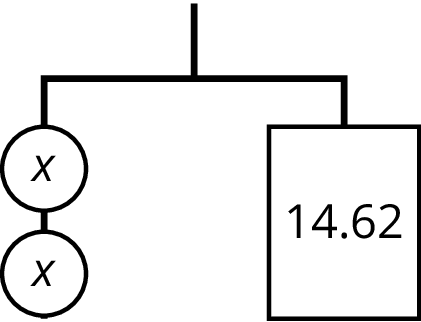
- Explain how to reason with the equation to find the value of $x$.
Problem 4
Andre says that $x$ is 7 because he can move the two 1s with the $x$ to the other side.
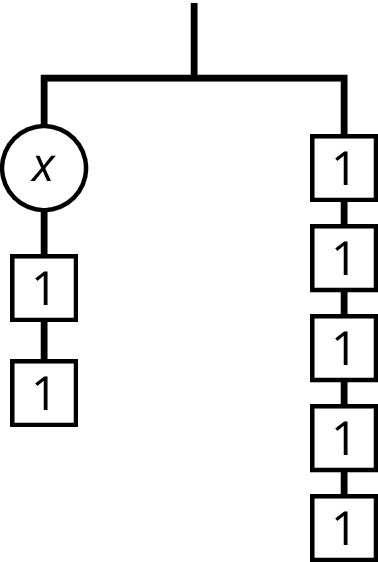
Do you agree with Andre? Explain your reasoning.
Problem 5 (from Unit 6, Lesson 1)
Match each equation to one of the diagrams.
- $12-m=4$
- $12=4m$
- $m-4=12$
- $\frac{m}{4}=12$

Problem 6 (from Unit 4, Lesson 13)
The area of a rectangle is 14 square units. It has side lengths $a$ and $b$. Given the following values for $a$, find $b$.
1. $a=2\frac13$
2. $a=4\frac15$
3. $a=\frac76$
Problem 7 (from Unit 3, Lesson 11)
Lin needs to save up \$20 for a new game. How much money does she have if she has saved the following percentages of her goal. Explain your reasoning.
- 25%
- 75%
- 125%
Lesson 4
Problem 1
Select all the equations that describe each situation and then find the solution.
-
Kiran’s backpack weighs 3 pounds less than Clare’s backpack. Clare’s backpack weighs 14 pounds. How much does Kiran’s backpack weigh?
-
$x+3=14$
-
$3x=14$
-
$x = 14 -3$
-
$x = 14 \div 3$
-
-
Each notebook contains 60 sheets of paper. Andre has 5 notebooks. How many sheets of paper do Andre’s notebooks contain?
-
$y = 60 \div 5$
-
$ y = 5 \boldcdot 60$
-
$\frac{y}{5} = 60$
-
$5y = 60$
-
Problem 2
Solve each equation.
- $2x = 5$
- $y + 1.8 = 14.7$
- $6 = \frac{1}{2} z$
- $3\frac{1}{4} = \frac{1}{2} + w$
- $2.5t = 10$
Problem 3 (from Unit 6, Lesson 1)
For each equation, draw a tape diagram that represents the equation.
- $3x = 18$
- $3+x=18$
- $17 - 6 = x$
Problem 4 (from Unit 5, Lesson 8)
Find each product.
- $(21.2)\boldcdot (0.02)$
- $(2.05)\boldcdot (0.004)$
Problem 5 (from Unit 3, Lesson 13)
For a science experiment, students need to find 25% of 60 grams. Jada says, “I can find this by calculating $\frac{1}{4}$ of 60.” Andre says, “25% of 60 means $\frac{25}{100} \boldcdot 60$.” Lin says both of their methods work. Do you agree with Lin? Explain your reasoning.
Lesson 5
Problem 1
Select all the expressions that equal $\frac{3.15}{0.45}$.
- $(3.15) \boldcdot (0.45)$
- $(3.15) \div (0.45)$
- $(3.15) \boldcdot \frac{1}{0.45}$
- $(3.15) \div \frac{45}{100}$
- $(3.15) \boldcdot \frac{100}{45}$
- $\frac{0.45}{3.15}$
Problem 2
Which expressions are solutions to the equation $\frac{3}{4}x = 15$? Select all that apply.
- $\frac{15}{\frac{3}{4}}$
- $\frac{15}{\frac{4}{3}}$
- $\frac{4}{3} \boldcdot 15$
- $\frac{3}{4} \boldcdot 15$
- $15 \div \frac{3}{4}$
Problem 3
Solve each equation.
- $4x = 32$
- $4=32x$
- $10x = 26$
- $26=100x$
Problem 4
For each equation, write a story problem represented by the equation. For each equation, state what quantity $x$ represents. If you get stuck, draw a diagram.
$\frac{3}{4} + x = 2$
$1.5x = 6$
Problem 5 (from Unit 3, Lesson 13)
Write as many mathematical expressions or equations as you can about the image. Include a fraction, a decimal number, or a percentage in each.

Problem 6 (from Unit 3, Lesson 12)
In a lilac paint mixture, 40% of the mixture is white paint, 20% is blue, and the rest is red. There are 4 cups of blue paint used in a batch of lilac paint.
- How many cups of white paint are used?
- How many cups of red paint are used?
- How many cups of lilac paint will this batch yield?
If you get stuck, consider using a tape diagram.
Problem 7 (from Unit 1, Lesson 9)
Triangle P has a base of 12 inches and a corresponding height of 8 inches. Triangle Q has a base of 15 inches and a corresponding height of 6.5 inches. Which triangle has a greater area? Show your reasoning.
Lesson 6
Problem 1
Instructions for a craft project say that the length of a piece of red ribbon should be 7 inches less than the length of a piece of blue ribbon.
-
How long is the red ribbon if the length of the blue ribbon is:
10 inches?
27 inches?
$x$ inches?
- How long is the blue ribbon if the red ribbon is 12 inches?
Problem 2
Tyler has 3 times as many books as Mai.
-
How many books does Mai have if Tyler has:
15 books?
21 books?
$x$ books?
- Tyler has 18 books. How many books does Mai have?
Problem 3
A bottle holds 24 ounces of water. It has $x$ ounces of water in it.
- What does $24-x$ represent in this situation?
- Write a question about this situation that has $24-x$ for the answer.
Problem 4 (from Unit 6, Lesson 1)
Write an equation represented by this tape diagram that uses each of the following operations.
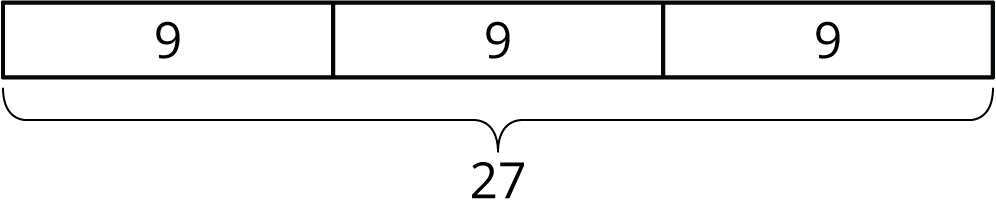
- addition
- subtraction
- multiplication
- division
Problem 5 (from Unit 6, Lesson 4)
Select all the equations that describe each situation and then find the solution.
-
Han's house is 450 meters from school. Lin’s house is 135 meters closer to school. How far is Lin’s house from school?
$z = 450 + 135$
$z = 450-135$
$z-135 = 450$
$z + 135 = 450$
-
Tyler's playlist has 36 songs. Noah’s playlist has one quarter as many songs as Tyler's playlist. How many songs are on Noah’s playlist?
$w = 4 \boldcdot 36$
$w = 36 \div 4$
$4w = 36$
$\frac{w}{4} = 36$
Problem 6 (from Unit 3, Lesson 12)
You had $50. You spent 10% of the money on clothes, 20% on games, and the rest on books. How much money was spent on books?
Problem 7 (from Unit 3, Lesson 14)
A trash bin has a capacity of 50 gallons. What percentage of its capacity is each of the following? Show your reasoning.
- 5 gallons
- 30 gallons
- 45 gallons
- 100 gallons
Lesson 7
Problem 1
A crew has paved $\frac{3}{4}$ of a mile of road. If they have completed 50% of the work, how long is the road they are paving?
Problem 2
40% of $x$ is 35.
- Write an equation that shows the relationship of 40%, $x$, and 35.
- Use your equation to find $x$. Show your reasoning.
Problem 3
Priya has completed 9 exam questions. This is 60% of the questions on the exam.
- Write an equation representing this situation. Explain the meaning of any variables you use.
- How many questions are on the exam? Show your reasoning.
Problem 4
Answer each question. Show your reasoning.
- 20% of $a$ is 11. What is $a$?
- 75% of $b$ is 12. What is $b$?
- 80% of $c$ is 20. What is $c$?
- 200% of $d$ is 18. What is $d$?
Problem 5 (from Unit 6, Lesson 2)
For the equation $2n - 3 = 7$
- What is the variable?
- What is the coefficient of the variable?
- Which of these is the solution to the equation? 2, 3, 5, 7, $n$
Problem 6 (from Unit 6, Lesson 2)
Which of these is a solution to the equation $\frac{1}{8}=\frac{2}{5} \boldcdot x$?
- $\frac{2}{40}$
- $\frac{5}{16}$
- $\frac{11}{40}$
- $\frac{17}{40}$
Problem 7 (from Unit 5, Lesson 13)
Find the quotients.
- $0.009 \div 0.001$
- $0.009 \div 0.002$
- $0.0045 \div 0.001$
- $0.0045 \div 0.002$
Lesson 8
Problem 1
- Draw a diagram of $x + 3$ and a diagram of $2x$ when $x$ is 1.

- Draw a diagram of $x+3$ and of $2x$ when $x$ is 2.

- Draw a diagram of $x+3$ and of $2x$ when $x$ is 3.

- Draw a diagram of $x+3$ and of $2x$ when $x$ is 4.

- When are $x+3$ and $2x$ equal? When are they not equal? Use your diagrams to explain.
Problem 2
- Do $4x$ and $15+x$ have the same value when $x$ is 5?
- Are $4x$ and $15+x$ equivalent expressions? Explain your reasoning.
Problem 3
- Check that $2b + b$ and $3b$ have the same value when $b$ is 1, 2, and 3.
- Do $2b +b$ and $3b$ have the same value for all values of $b$? Explain your reasoning.
- Are $2b+b$ and $3b$ equivalent expressions?
Problem 4 (from Unit 6, Lesson 7)
80% of $x$ is equal to 100.
- Write an equation that shows the relationship of 80%, $x$, and 100.
- Use your equation to find $x$.
Problem 5 (from Unit 6, Lesson 5)
For each story problem, write an equation to represent the problem and then solve the equation. Be sure to explain the meaning of any variables you use.
- Jada’s dog was $5\frac{1}{2}$ inches tall when it was a puppy. Now her dog is $14\frac{1}{2}$ inches taller than that. How tall is Jada’s dog now?
- Lin picked $9 \frac{3}{4}$ pounds of apples, which was 3 times the weight of the apples Andre picked. How many pounds of apples did Andre pick?
Lesson 9
Problem 1
Select all the expressions that represent the area of the large, outer rectangle.
- $5(2+4)$
- $5 \boldcdot 2 + 4$
- $5 \boldcdot 2 + 5 \boldcdot 4$
- $5 \boldcdot 2 \boldcdot 4$
- $5 + 2+ 4$
- $5 \boldcdot 6$
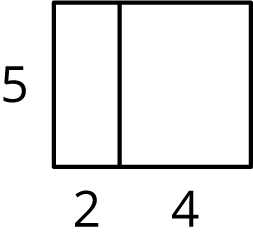
Problem 2
Draw and label diagrams that show these two methods for calculating $19 \boldcdot 50$.
- First find $10\boldcdot 50$ and then add $9 \boldcdot 50$.
- First find $20 \boldcdot 50$ and then take away 50.
Problem 3
$$98 \boldcdot 24$$ $$(100-2) \boldcdot 24$$ $$\ldots$$
$$21 \boldcdot 15$$ $$(20 + 1) \boldcdot 15$$ $$\ldots$$
$$0.51 \boldcdot 40$$ $$(0.5 + 0.01) \boldcdot 40$$ $$\ldots$$
Problem 4
Problem 5 (from Unit 6, Lesson 8)
- On graph paper, draw diagrams of $a+a+a+a$ and $4a$ when $a$ is 1, 2, and 3. What do you notice?
- Do $a+a+a+a$ and $4a$ have the same value for any value of $a$? Explain how you know.
Problem 6 (from Unit 6, Lesson 7)
120% of $x$ is equal to 78.
- Write an equation that shows the relationship of 120%, $x$, and 78.
- Use your equation to find $x$. Show your reasoning.
Problem 7 (from Unit 6, Lesson 6)
Kiran’s aunt is 17 years older than Kiran.
- How old will Kiran’s aunt be when Kiran is:
15 years old?
30 years old?
$x$ years old?
- How old will Kiran be when his aunt is 60 years old?
Lesson 10
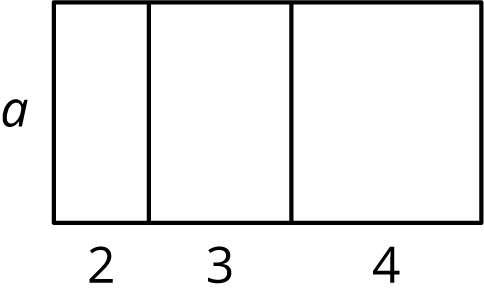
Problem 1
Here is a rectangle.
- Explain why the area of the large rectangle is $2a + 3a + 4a$.
- Explain why the area of the large rectangle is $(2+3+4)a$.
Problem 2
Is the area of the shaded rectangle $6(2-m)$ or $6(m-2)$?
Explain how you know.

Problem 3
Choose the expressions that do not represent the total area of the rectangle. Select all that apply.
- $5t + 4t$
- $t + 5 + 4$
- $9t$
- $4 \boldcdot 5 \boldcdot t$
- $t(5+4)$
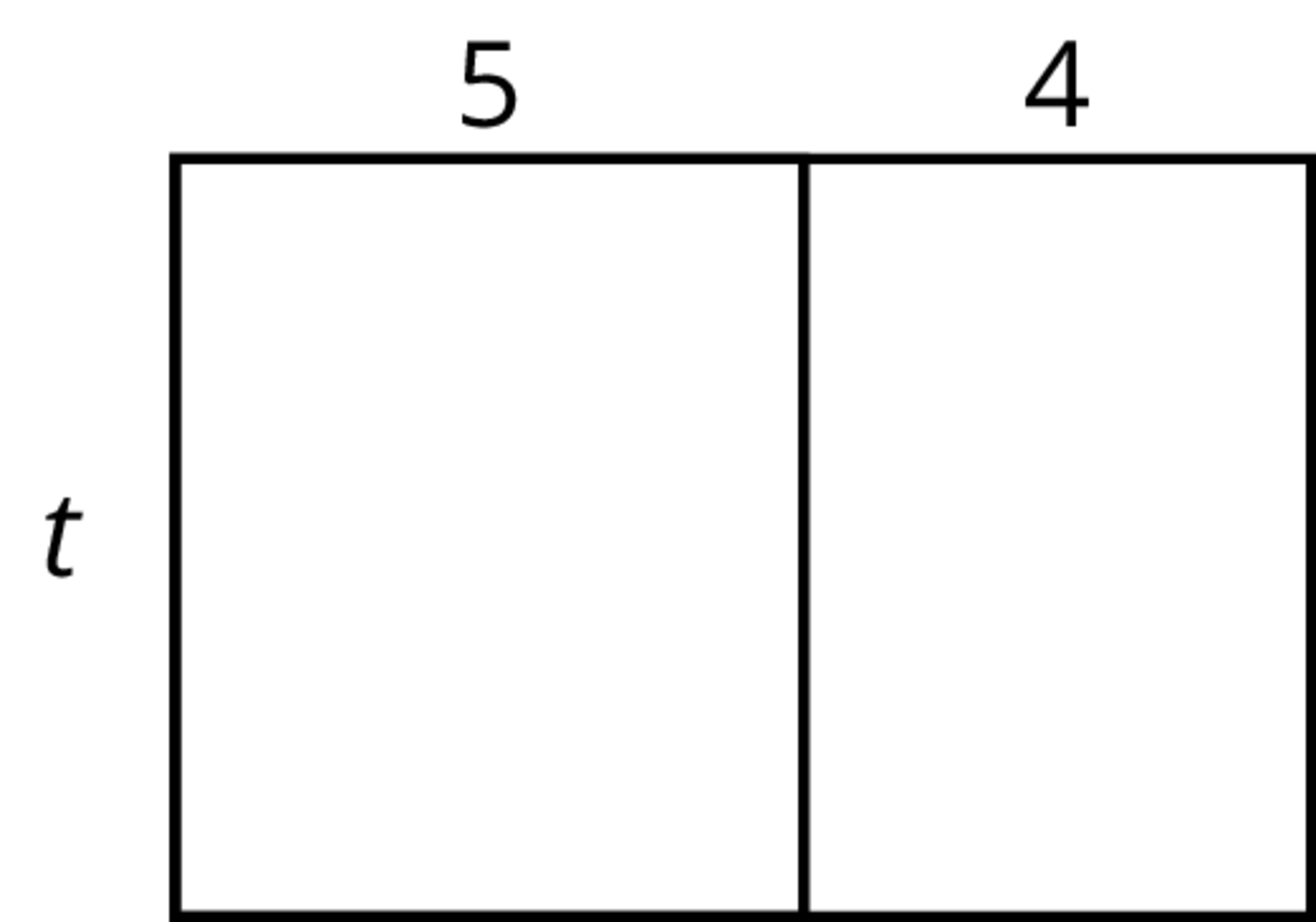
Problem 4 (from Unit 6, Lesson 9)
Evaluate each expression mentally.
- $35\boldcdot 91-35\boldcdot 89$
- $22\boldcdot 87+22\boldcdot 13$
- $\frac{9}{11}\boldcdot \frac{7}{10}-\frac{9}{11}\boldcdot \frac{3}{10}$
Problem 5 (from Unit 6, Lesson 8)
Select all the expressions that are equivalent to $4b$.
- $b+b+b+b$
- $b+4$
- $2b+2b$
- $b \boldcdot b \boldcdot b \boldcdot b$
- $b \div \frac{1}{4}$
Problem 6 (from Unit 6, Lesson 4)
Solve each equation. Show your reasoning.
- $111=14g$
- $13.65 = h + 4.88$
- $k+ \frac{1}{3} = 5\frac{1}{8}$
- $\frac{2}{5} m = \frac{17}{4}$
- $5.16 = 4n$
Problem 7 (from Unit 6, Lesson 2)
Andre ran $5\frac{1}{2}$ laps of a track in 8 minutes at a constant speed. It took Andre $x$ minutes to run each lap. Select all the equations that represent this situation.
- $\left(5\frac{1}{2}\right)x = 8$
- $5 \frac{1}{2} + x = 8$
- $5 \frac{1}{2} - x = 8$
- $5 \frac{1}{2} \div x = 8$
- $x = 8 \div \left(5\frac{1}{2}\right)$
- $x = \left(5\frac{1}{2}\right) \div 8$
Lesson 11
Problem 1
For each expression, use the distributive property to write an equivalent expression.
- $4(x+2)$
- $(6+8)\boldcdot x$
- $4(2x+3)$
- $6(x+y+z)$
Problem 2
Priya rewrites the expression $8y - 24$ as $8(y-3)$. Han rewrites $8y-24$ as $2(4y-12)$. Are Priya's and Han's expressions each equivalent to $8y-24$? Explain your reasoning.
Problem 3
Select all the expressions that are equivalent to $16x + 36$.
- $16(x+20)$
- $x(16+36)$
- $4(4x+9)$
- $2(8x+18)$
- $2(8x+36)$
Problem 4
Problem 5 (from Unit 6, Lesson 8)
Select all the expressions that are equivalent to $\frac{1}{2}z$.
- $z + z$
- $z \div 2$
- $z \boldcdot z$
- $\frac{1}{4}z + \frac{1}{4} z$
- $2z$
Problem 6 (from Unit 6, Lesson 6)
-
What is the perimeter of a square with side length:
$3$ cm
$7$ cm
$s$ cm
- If the perimeter of a square is 360 cm, what is its side length?
-
What is the area of a square with side length:
$3$ cm
$7$ cm
$s$ cm
- If the area of a square is 121 cm2, what is its side length?
Problem 7 (from Unit 6, Lesson 5)
Solve each equation.
- $10=4y$
- $5y = 17.5$
- $1.036=10y$
- $0.6y = 1.8$
- $15=0.1y$
Lesson 12
Problem 1
Select all expressions that are equivalent to 64.
- $2^6$
- $2^8$
- $4^3$
- $8^2$
- $16^4$
- $32^2$
Problem 2
Select all the expressions that equal $3^4$.
- 7
- $4^3$
- 12
- 81
- 64
- $9^2$
Problem 3
$4^5$ is equal to 1,024. Evaluate the following expressions.
- $4^6$
- $4^4$
- $4^3\boldcdot 4^2$
Problem 4
$6^3=216$. Using exponents, write three more expressions whose value is 216.
Problem 5 (from Unit 6, Lesson 11)
Problem 6 (from Unit 6, Lesson 5)
Solve each equation.
- $a - 2.01 = 5.5$
- $b + 2.01 = 5.5$
- $10c = 13.71$
- $100d = 13.71$
Problem 7 (from Unit 6, Lesson 10)
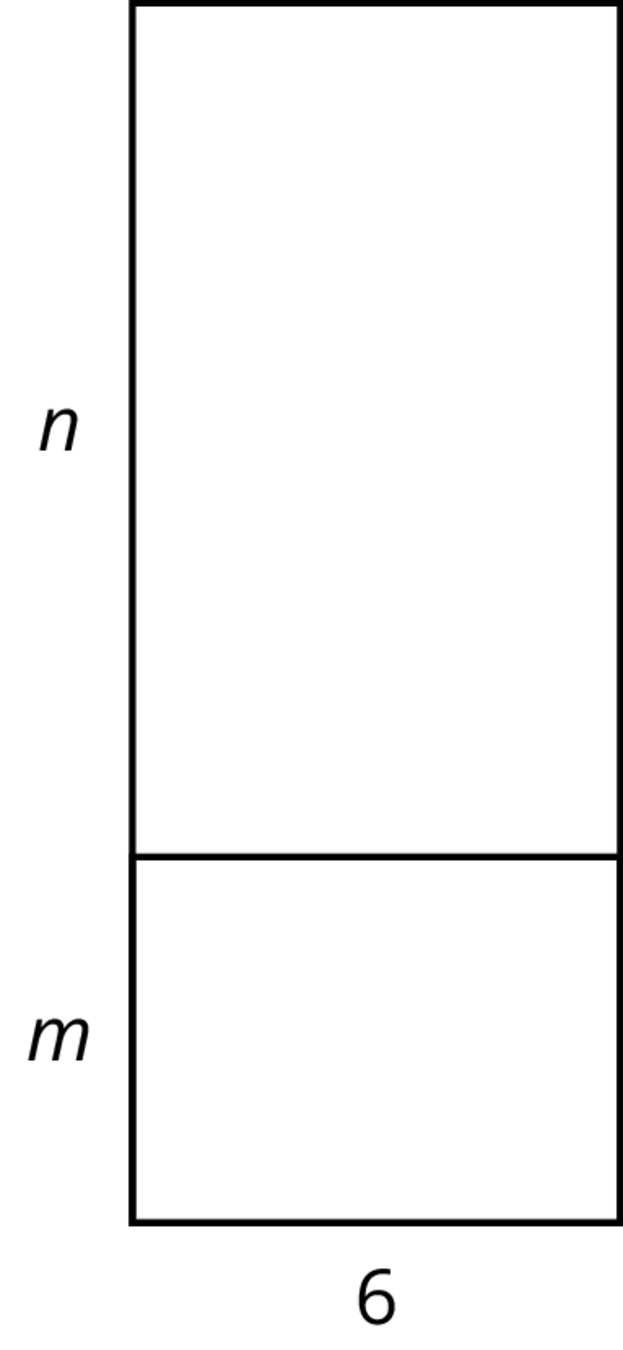
Which expressions represent the total area of the large rectangle? Select all that apply.
- $6(m+n)$
- $6n + m$
- $6n + 6m$
- $6mn$
- $(n+m)6$
Problem 8 (from Unit 3, Lesson 16)
Is each statement true or false? Explain your reasoning.
- $\frac{45}{100} \boldcdot 72 = \frac{45}{72} \boldcdot 100$
- 16% of 250 is equal to 250% of 16
Lesson 13
Problem 1
Select all expressions that are equal to $3 \boldcdot 3 \boldcdot 3 \boldcdot 3 \boldcdot 3$.
- $3 \boldcdot 5$
- $3^5$
- $3^4 \boldcdot 3$
- $5 \boldcdot 3$
- $5^3$
Problem 2
Noah starts with 0 and then adds the number 5 four times. Diego starts with 1 and then multiplies by the number 5 four times. For each expression, decide whether it is equal to Noah’s result, Diego’s result, or neither.
- $4 \boldcdot 5$
- $4+5$
- $4^5$
- $5^4$
Problem 3
Decide whether each equation is true or false, and explain how you know.
- $9 \boldcdot 9 \boldcdot 3 = 3^5$
- $7 + 7 + 7 = 3 + 3 + 3 + 3 + 3 + 3 + 3$
- $\frac{1}{7} \boldcdot \frac{1}{7} \boldcdot \frac{1}{7} = \frac{3}{7}$
- $4^1 = 4 \boldcdot 1$
-
$6 + 6 + 6 = 6^3$
Problem 4
- What is the area of a square with side lengths of $\frac35$ units?
- What is the side length of a square with area $\frac{1}{16}$ square units?
- What is the volume of a cube with edge lengths of $\frac23$ units?
- What is the edge length of a cube with volume $\frac{27}{64}$ cubic units?
Problem 5 (from Unit 6, Lesson 10)
Select all the expressions that represent the area of the shaded rectangle.
- $3(10-c)$
- $3(c-10)$
- $10(c-3)$
- $10(3-c)$
- $30-3c$
- $30-10c$

Problem 6 (from Unit 5, Lesson 13)
A ticket at a movie theater costs \$8.50. One night, the theater had \$29,886 in ticket sales.
-
Estimate about how many tickets the theater sold. Explain your reasoning.
-
How many tickets did the theater sell? Explain your reasoning.
Problem 7 (from Unit 4, Lesson 12)
A fence is being built around a rectangular garden that is $8 \frac{1}{2}$ feet by $6 \frac{1}{3}$ feet. Fencing comes in panels. Each panel is $\frac{2}{3}$ of a foot wide. How many panels are needed? Explain or show your reasoning.
Lesson 14
Problem 1
Lin says, “I took the number 8, and then multiplied it by the square of 3.” Select all expressions that equal Lin’s answer.
- $8 \boldcdot 3^2$
- $(8 \boldcdot 3)^2$
- $8 \boldcdot 2^3$
- $3^2 \boldcdot 8$
- $24^2$
- 72
Problem 2
Evaluate each expression.
- $7 + 2^3$
- $9 \boldcdot 3^1$
- $20 - 2^4$
- $2 \boldcdot 6^2$
- $8 \boldcdot (\frac{1}{2})^2$
- $\frac{1}{3} \boldcdot 3^3$
- $(\frac{1}{5} \boldcdot 5)^5$
Problem 3
Andre says, “I multiplied 4 by 5, then cubed the result.” Select all expressions that equal Andre’s answer.
- $4 \boldcdot 5^3$
- $(4 \boldcdot 5)^3$
- $(4 \boldcdot 5)^2$
- $5^3 \boldcdot 4$
- $20^3$
- 500
- 8,000
Problem 4
Han has 10 cubes, each 5 inches on a side.
- Find the total volume of Han’s cubes. Express your answer as an expression using an exponent.
-
Find the total surface area of Han’s cubes. Express your answer as an expression using an exponent.
Problem 5 (from Unit 6, Lesson 13)
Priya says that $\frac{1}{3} \boldcdot \frac{1}{3} \boldcdot \frac{1}{3} \boldcdot \frac{1}{3} = \frac{4}{3}$. Do you agree with Priya? Explain or show your reasoning.
Problem 6 (from Unit 6, Lesson 7)
Answer each question. Show your reasoning.
- 125% of $e$ is 30. What is $e$?
- 35% of $f$ is 14. What is $f$?
Problem 7 (from Unit 6, Lesson 5)
Which expressions are solutions to the equation $2.4y = 13.75$? Select all that apply.
- $13.75 - 1.4$
- $13.75 \boldcdot 2.4$
- $13.75 \div 2.4$
- $\frac{13.75}{2.4}$
- $2.4 \div 13.75$
Problem 8 (from Unit 5, Lesson 7)
Jada explains how she finds $15 \boldcdot 23$:
“I know that ten 23s is 230, so five 23s will be half of 230, which is 115. 15 is 10 plus 5, so $15 \boldcdot 23$ is 230 plus 115, which is 345.”
-
Do you agree with Jada? Explain.
-
Draw a 15 by 23 rectangle. Partition the rectangle into two rectangles and label them to show Jada’s reasoning.
Lesson 15
Problem 1
Evaluate the following expressions if $x=3$.
- $2^x$
- $x^2$
- $1^x$
- $x^1$
- $\left(\frac12\right)^x$
Problem 2
Evaluate each expression for the given value of $x$.
- $2 + x^3$, $x$ is 3
- $x^2$, $x$ is $\frac{1}{2}$
- $3x^2$, $x$ is 5
- $100 - x^2$, $x$ is 6
Problem 3
Decide if the expressions have the same value. If not, determine which expression has the larger value.
- $2^3$ and $3^2$
- $1^{31}$ and $31^1$
- $4^2$ and $2^4$
- $\left(\frac12\right)^3$ and $\left(\frac13\right)^2$
Problem 4
Match each equation to its solution.
- $7 + x^2 = 16$
- $5 - x^2 = 1$
- $2 \boldcdot 2^3 = 2^x$
- $\frac{3^4}{3^x}=27$
- $x=4$
- $x=1$
- $x=2$
- $x=3$
Problem 5 (from Unit 6, Lesson 6)
An adult pass at the amusement park costs 1.6 times as much as a child’s pass.
-
How many dollars does an adult pass cost if a child’s pass costs:
\$5?
\$10?
$w$
- A child’s pass costs \$15. How many dollars does an adult pass cost?
Problem 6 (from Unit 2, Lesson 14)
Jada reads 5 pages every 20 minutes. At this rate, how many pages can she read in 1 hour?
- Use a double number line to find the answer.
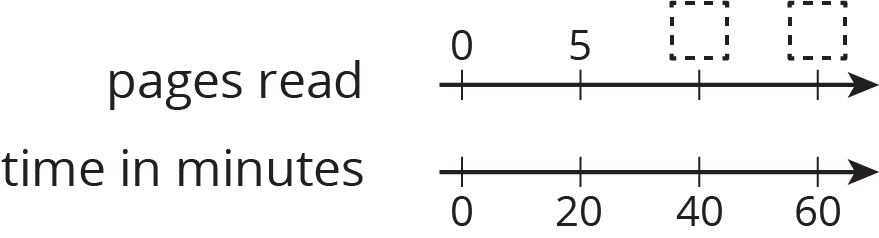
- Use a table to find the answer.
| pages read | time in minutes | |
|---|---|---|
| row 1 | 5 | 20 |
| row 2 | ||
| row 3 |
- Explain which strategy you thinks works better in finding the answer.
Lesson 16
Problem 1
Here is a graph that shows some values for the number of cups of sugar, $s$, required to make $x$ batches of brownies.
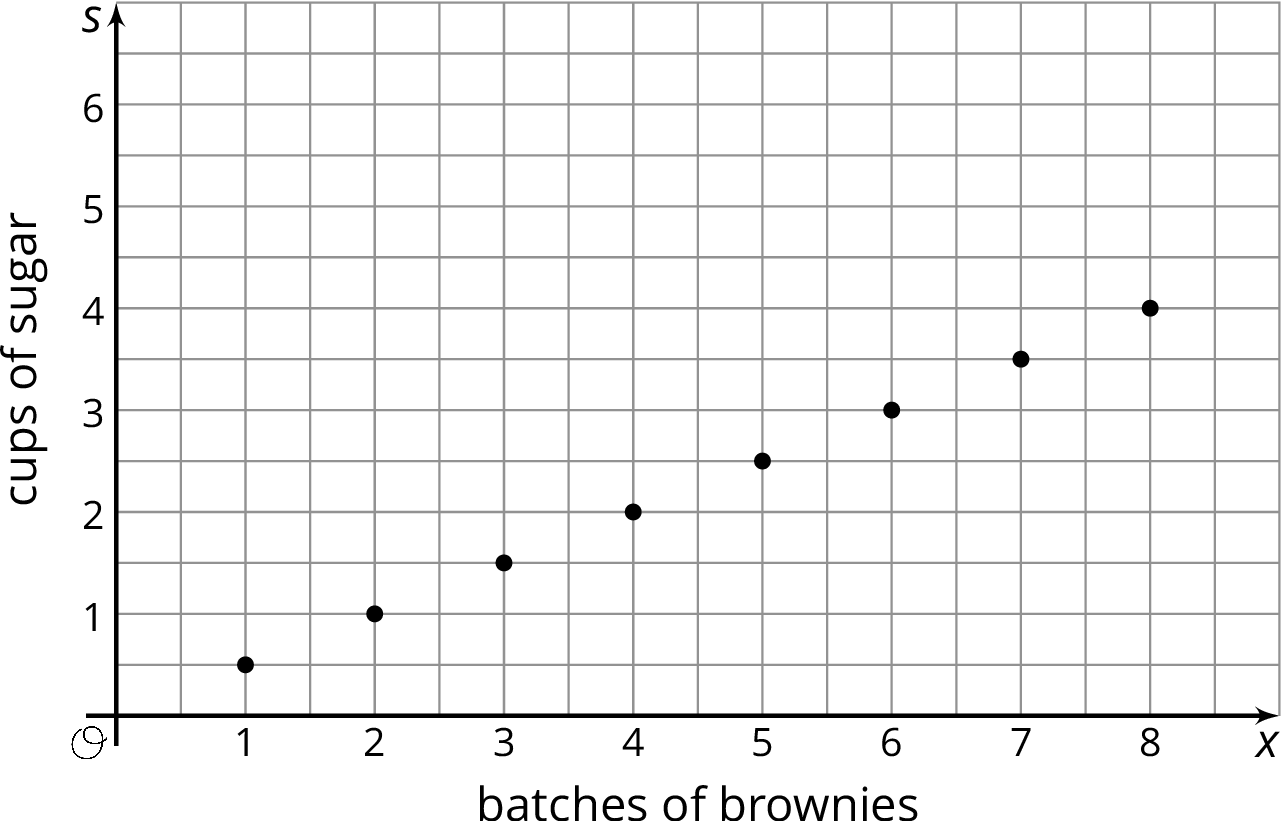
- Complete the table so that the pair of numbers in each column represents the coordinates of a point on the graph.
$x$ 1 2 3 4 5 6 7 row 1 $s$
- What does the point $(8,4)$ mean in terms of the amount of sugar and number of batches of brownies?
- Write an equation that shows the amount of sugar in terms of the number of batches.
Problem 2
Each serving of a certain fruit snack contains 90 calories.
- Han wants to know how many calories he gets from the fruit snacks. Write an equation that shows the number of calories, $c$, in terms of the number of servings, $n$.
- Tyler needs some extra calories each day during his sports season. He wants to know how many servings he can have each day if all the extra calories come from the fruit snack. Write an equation that shows the number of servings, $n$, in terms of the number of calories, $c$.
Problem 3
Kiran shops for books during a 20% off sale.
- What percent of the original price of a book does Kiran pay during the sale?
- Complete the table to show how much Kiran pays for books during the sale.
- Write an equation that relates the sale price, $s$, to the original price $p$.
- On graph paper, create a graph showing the relationship between the sale price and the original price by plotting the points from the table.
| original price in dollars $(s)$ |
sale price in dollars $(p)$ |
|
|---|---|---|
| row 1 | 1 | |
| row 2 | 2 | |
| row 3 | 3 | |
| row 4 | 4 | |
| row 5 | 5 | |
| row 6 | 6 | |
| row 7 | 7 | |
| row 8 | 8 | |
| row 9 | 9 | |
| row 10 | 10 |
Lesson 17
Problem 1
A car is traveling down a road at a constant speed of 50 miles per hour.
- Complete the table with the amounts of time it takes the car to travel certain distances, or the distances traveled for certain amounts of time.
-
Write an equation that represents the distance traveled by the car, $d$, for an amount of time, $t$.
- In your equation, which is the dependent variable and which is the independent variable?
| time (hours) | distance (miles) | |
|---|---|---|
| row 1 | 2 | |
| row 2 | 1.5 | |
| row 3 | $t$ | |
| row 4 | 50 | |
| row 5 | 300 | |
| row 6 | $d$ |
Problem 2
The graph represents the amount of time in hours it takes a ship to travel various distances in miles.
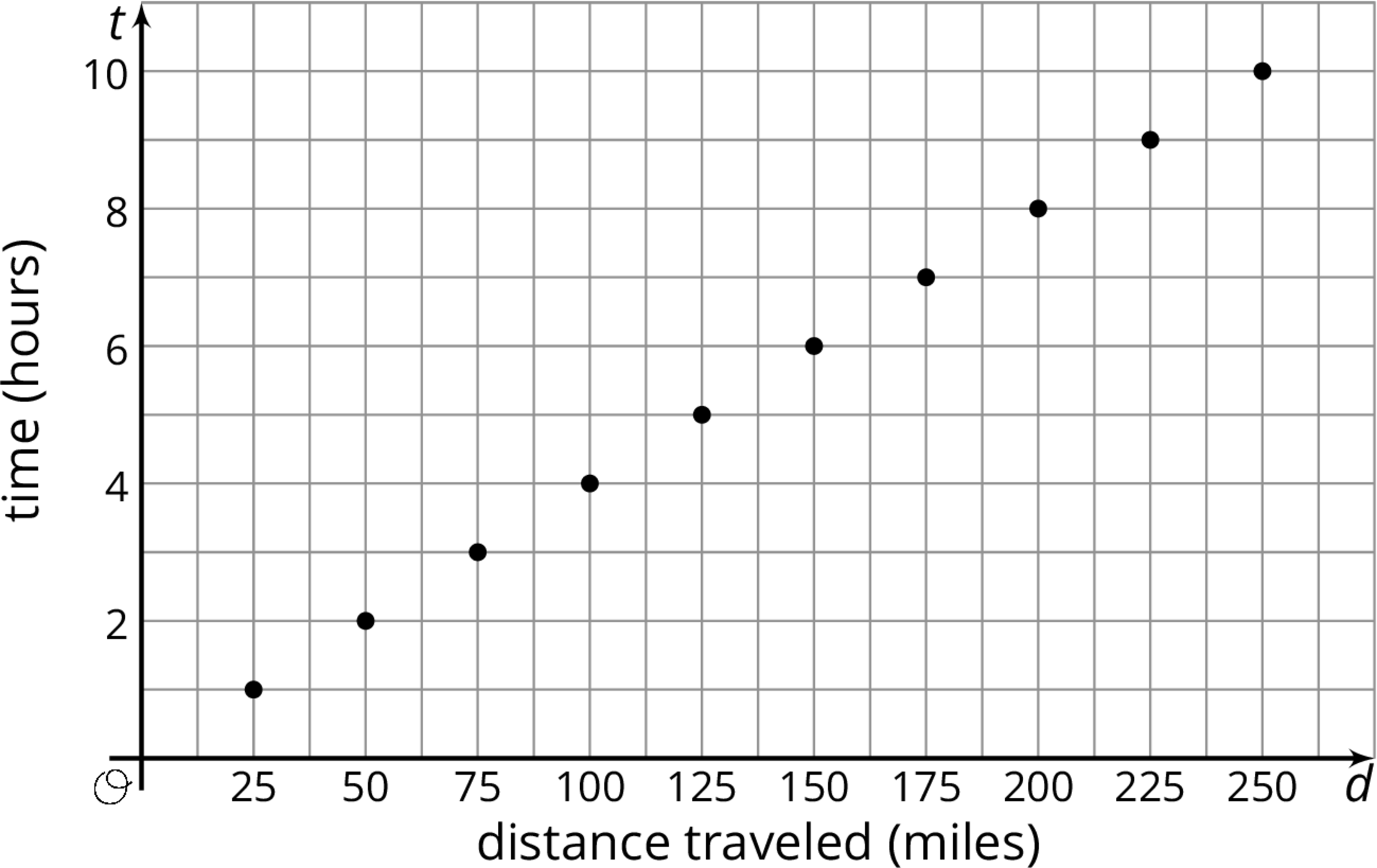
- Write the coordinates of one of point on the graph. What does the point represent?
- What is the speed of the ship in miles per hour?
- Write an equation that relates the time, $t$, it takes to travel a given distance, $d$.
Problem 3 (from Unit 6, Lesson 15)
Find a solution to each equation in the list that follows (not all numbers will be used):
- $2^x=8$
- $2^x=2$
- $x^2=100$
- $x^2=\frac{1}{100}$
- $x^1=7$
- $2^x\boldcdot 2^3=2^7$
- $\frac{2^x}{2^3}=2^5$
List:
$\frac{1}{10}$
$\frac{1}{3}$
1
2
3
4
5
7
8
10
16
Problem 4 (from Unit 6, Lesson 11)
Select all the expressions that are equivalent to $5x +30x - 15x$.
- $5(x + 6x-3x)$
- $(5+30-15)\boldcdot x$
- $x(5+30x-15x)$
- $5x(1+6-3)$
- $5(x+30x-15x)$
Lesson 18
Problem 1
Elena is designing a logo in the shape of a parallelogram. She wants the logo to have an area of 12 square inches. She draws bases of different lengths and tries to compute the height for each.
- Write an equation Elena can use to find the height, $h$, for each value of the base, $b$.
- Use your equation to find the height of a parallelogram with base $1.5$ inches.
Problem 2
Han is planning to ride his bike 24 miles.
-
If he rides at a rate of 3 miles per hour, how long will it take?
At 4 miles per hour?
At 6 miles per hour?
- Write an equation that Han can use to find $t$, the time it will take to ride 24 miles, if his rate in miles per hour is represented by $r$.
- On graph paper, draw a graph that shows $t$ in terms of $r$ for a 24-mile ride.
Problem 3
The graph of the equation $V=10s^3$ contains the points $(2,80)$ and $(4,640)$.
- Create a story that is represented by this graph.
- What do the points mean in the context of your story?
Problem 4
You find a brass bottle that looks really old. When you rub some dirt off of the bottle, a genie appears! The genie offers you a reward. You must choose one:
- \$50,000; or
- A magical \$1 coin. The coin will turn into two coins on the first day. The two coins will turn into four coins on the second day. The four coins will double to 8 coins on the third day. The genie explains the doubling will continue for 28 days.
- Write an equation that shows the number of coins, $n$, in terms of the day, $d$.
- Create a table that shows the number of coins for each day for the first 15 days.
- Create a graph for days 7 through 12 that shows how the number of coins grows with each day.