Lesson 4: Parallelograms

Let’s investigate the features and area of parallelograms.

4.1: Features of a Parallelogram

Figures A, B, and C are parallelograms. Figures D, E, and F are not parallelograms. 

Six figures on a grid labeled A--F.

Study the examples and non-examples. What do you notice about:

  1. the number of sides that a parallelogram has?
  2. opposite sides of a parallelogram?
  3. opposite angles of a parallelogram?

4.2: Area of a Parallelogram

  1. Find the area of the parallelogram and explain your reasoning.

GeoGebra Applet kj5DcRvn

  1. Change the parallelogram by dragging the green points at its vertices. Find its area and explain your reasoning.

GeoGebra Applet AhaRCfWA

  1. If you used the polygons on the side, how were they helpful? If you did not, could you use one or more of the polygons to show another way to find the area of the parallelogram?

4.3: Lots of Parallelograms

Find the area of the following parallelograms. Show your reasoning.

Two figures on a grid: parallelogram A and parallelogram B.
Parallelogram C has base 6, height 4, and diagonal length 4.5.

Summary

A parallelogram is a quadrilateral (it has four sides). The opposite sides of a parallelogram are parallel. It is also true that:

  • The opposite sides of a parallelogram have equal length.
  • The opposite angles of a parallelogram have equal measure.
“”

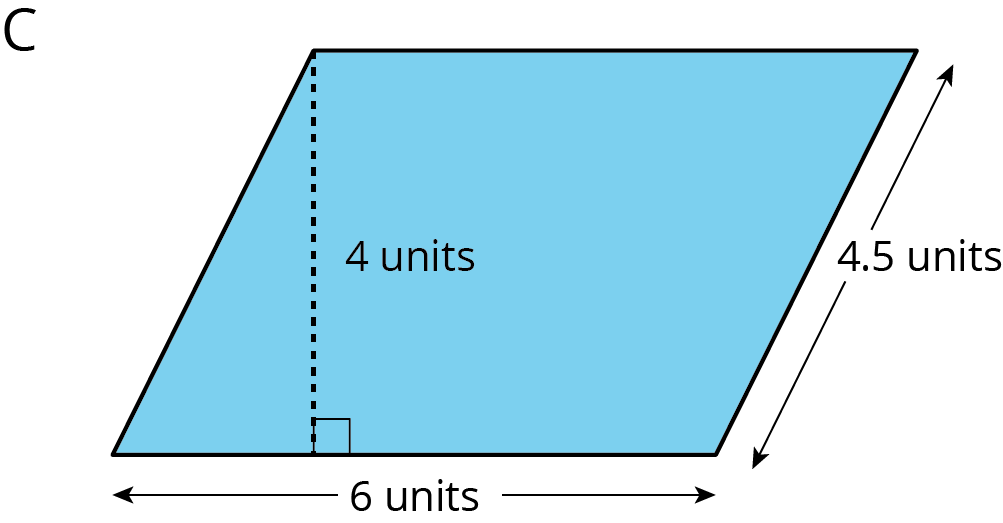
There are several strategies for finding the area of a parallelogram.

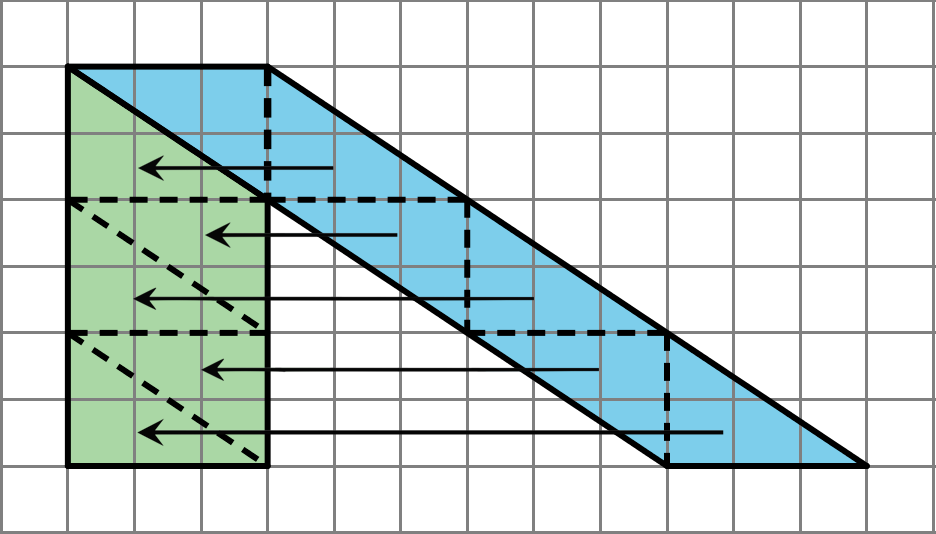
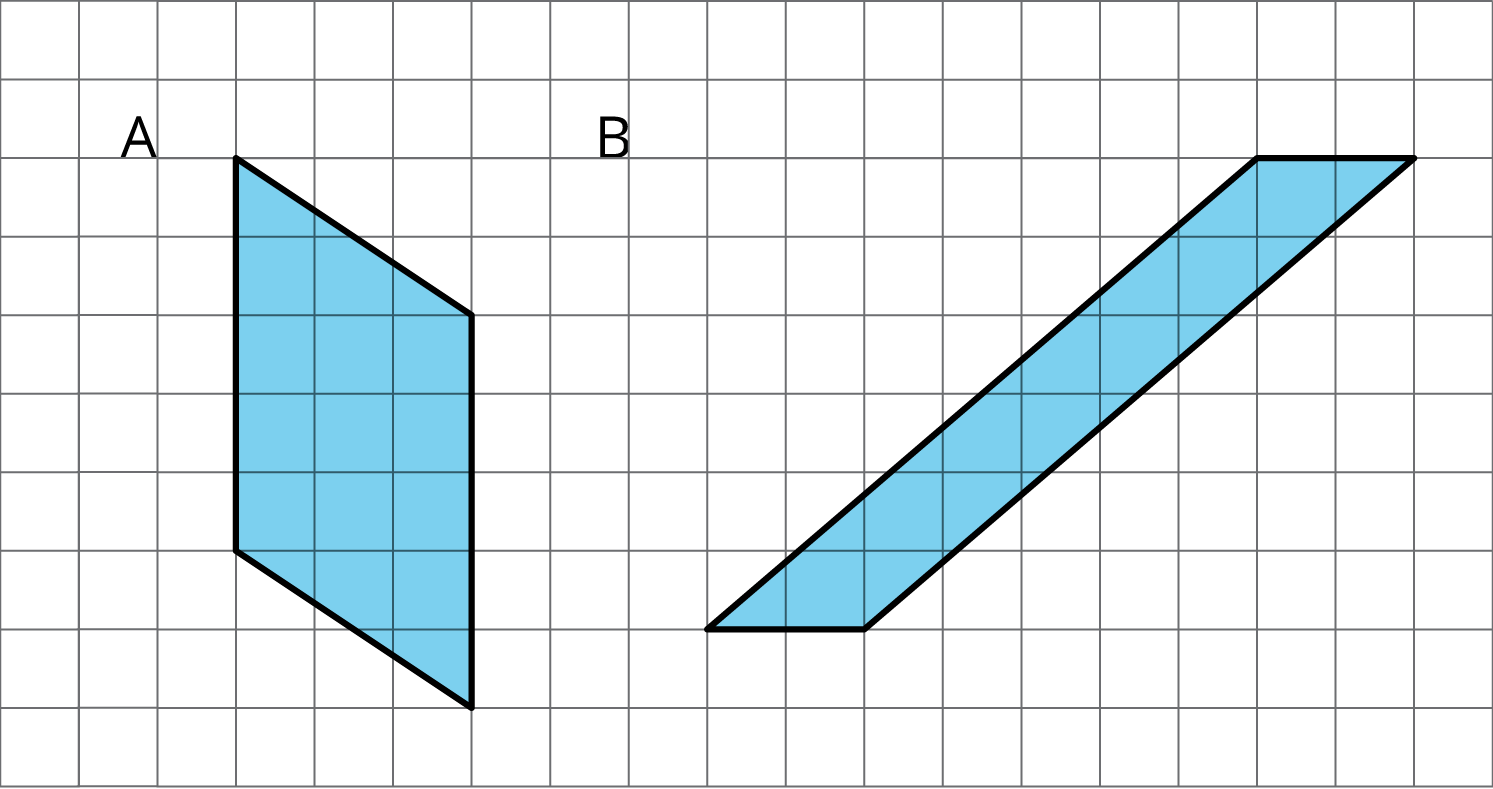
  • We can decompose and rearrange a parallelogram to form a rectangle. Here are three ways:
    Three identical parallelograms with horizontal sides that are four units long, drawn in grids. The first parallelogram has a perpendicular segment extending from 2 units in from the top left down to the vertex of the bottom horizontal side. An arrow extends from the resulting triangle to the opposite side of the parallelogram to create a rectangle measuring 4 units wide and 3 units high. The second parallelogram has a perpendicular segment extending from 2 units in from the bottom right up to the vertex of the top horizontal side. An arrow extends from the resulting triangle to the opposite side of the parallelogram to create a rectangle measuring 4 units wide and 3 units high. The third parallelogram has a perpendicular segment extending from 3 units in from the bottom right up to the vertex of the top horizontal side. An arrow extends from the resulting shape to the opposite side of the parallelogram to create a rectangle measuring 4 units wide and 3 units high.
  • We can enclose the parallelogram and then subtract the area of the two triangles in the corner.
    “”

Both of these ways will work for any parallelogram.

For some parallelograms, however, the process of decomposing and rearranging requires a lot more steps than if we enclose the parallelogram with a rectangle and subtract the combined area of the two triangles in the corners. Here is an example.

A shaded parallelogram drawn on a grid, with a base of three units angled sides that decline 6 vertical units over 9 horizontal units. The parallelogram is divided by dashed segments into six equal right triangles, triangle has one side that is 2 units and another that is 3 units. Arrows extend to the left from each of the lower 5 triangles. The resulting shape is a rectangle that is 6 units tall by 3 units wide.

Practice Problems ▶

Glossary

parallelogram

parallelogram

A parallelogram is a four-sided polygon with two pairs of parallel sides.