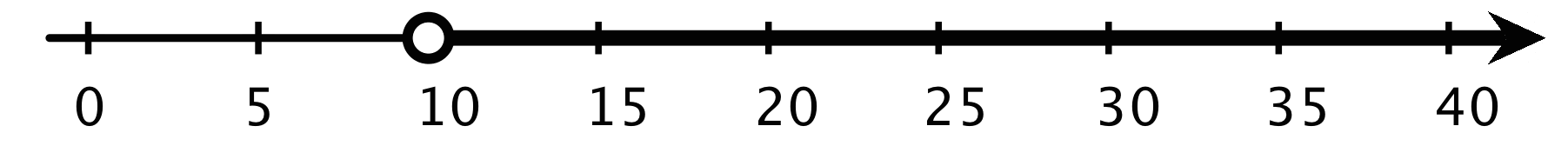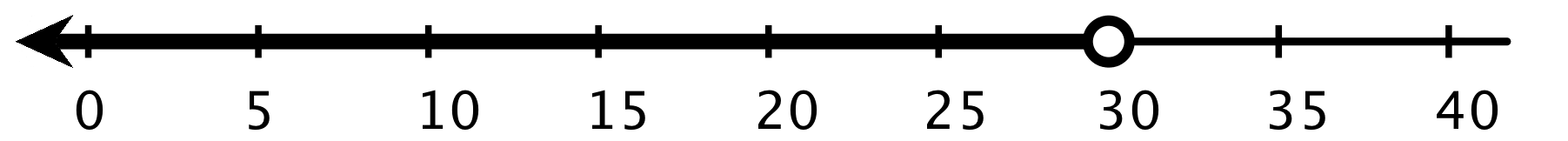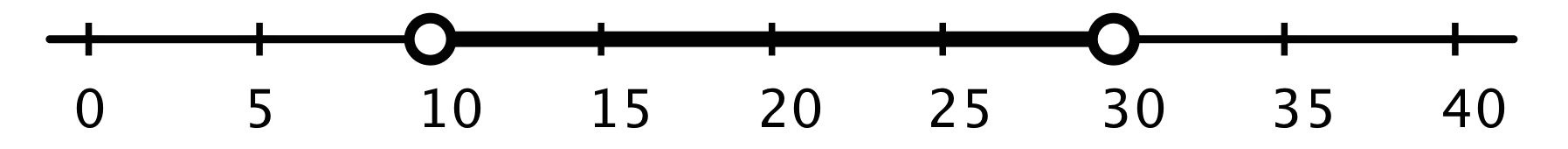Lesson 9: Solutions of Inequalities

Let’s think about the solutions to inequalities.

9.1: Unknowns on a Number Line

The number line shows several points, each labeled with a letter.

A number line with the number 0 indicated in the middle. Points A, B, C, D, E and F appear along the number line, with point D indicated at 0. Points A and F are located on opposite sides of point D with point A far to the left and point F far to the right of point D with Point F being closer to point D than point A. Point B is located less than halfway between point A and point D. Point C is located about halfway between the points B and D with it being closer to point D. Point E is located about halfway between points D and F with it being closer to point F. Points B and E are located about an equal distance from point D.

  1. Fill in each blank with a letter so that the inequality statements are true.

    a. _______ > _______

    b. _______ < _______

  2. Jada says that she found three different ways to complete the first question correctly. Do you think this is possible? Explain your reasoning.
  3. List a possible value for each letter on the number line based on its location.

9.2: Amusement Park Rides

Priya finds these height requirements for some of the rides at an amusement park.

  to ride the . . .  you must be . . . 
row 1 High Bounce between 55 and 72 inches tall
row 2 Climb-A-Thon under 60 inches tall
row 3 Twirl-O-Coaster 58 inches minimum

  1. Write an inequality for each of the the three height requirements. Use $h$ for the unknown height. Then, represent each height requirement on a number line. 

    High Bounce

    A blank number line with 17 evenly spaced tick marks.

    Climb-A-Thon

    A blank number line with 17 evenly spaced tick marks.

    Twirl-O-Coaster

    A blank number line with 17 evenly spaced tick marks.

    Pause here for additional instructions from your teacher.

  2. Han’s cousin is 55 inches tall. Han doesn’t think she is tall enough to ride the High Bounce, but Kiran believes that she is tall enough. Do you agree with Han or Kiran? Be prepared to explain your reasoning.

  3. Priya can ride the Climb-A-Thon, but she cannot ride the High Bounce or the Twirl-O-Coaster. Which, if any, of the following could be Priya’s height? Be prepared to explain your reasoning.

    59 inches

    53 inches

    56 inches

  4. Jada is 56 inches tall. Which rides can she go on? 
  5. Kiran is 60 inches tall. Which rides can he go on? 
  6. The inequalities $h < 75$ and $h > 64$ represent the height restrictions, in inches, of another ride. Write three values that are solutions to both of these inequalities.

9.3: What Number Am I?

Your teacher will give your group two sets of cards—one set shows inequalities and the other shows numbers. Arrange the inequality cards face up where everyone can see them. Stack the number cards face down and shuffle them.

To play:

  • Nominate one member of your group to be the detective. The other three players are clue givers.

  • One clue giver picks a number from the stack and shows it only to the other clue givers. Each clue giver then chooses an inequality that will help the detective identify the unknown number.

  • The detective studies the inequalities and makes three guesses.

  • If the detective cannot guess the number correctly, the clue givers must choose an additional inequality to help. Add as many inequalities as needed to help the detective identify the correct number.

  • When the detective succeeds, a different group member becomes the detective and everyone else is a clue giver.

  • Repeat the game until everyone has had a turn playing the detective.

Summary

Let’s say a movie ticket costs less than \$10. If $c$ represents the cost of a movie ticket, we can use $c < 10$ to express what we know about the cost of a ticket.

Any value of $c$ that makes the inequality true is called a solution to the inequality.

For example, 5 is a solution to the inequality $c < 10$ because $5<10$ (or “5 is less than 10”) is a true statement, but 12 is not a solution because $12<10$ (“12 is less than 10”) is not a true statement.

If a situation involves more than one boundary or limit, we will need more than one inequality to express it.

For example, if we knew that it rained for more than 10 minutes but less than 30 minutes, we can describe the number of minutes that it rained ($r$) with the following inequalities and number lines. $$r > 10$$

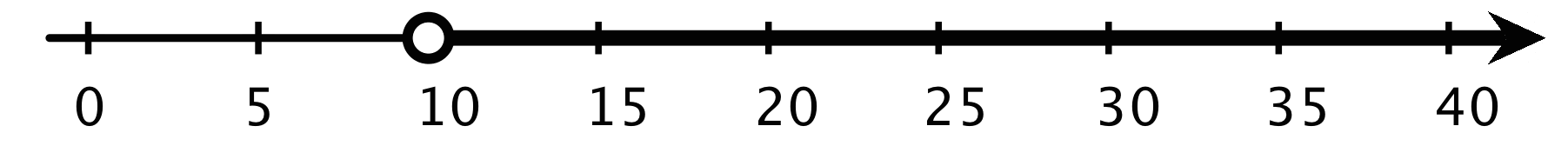$$r < 30$$
 

Any number of minutes greater than 10 is a solution to $r>10$, and any number less than 30 is a solution to $r<30$. But to meet the condition of “more than 10 but less than 30,” the solutions are limited to the numbers between 10 and 30 minutes, not including 10 and 30.

We can show the solutions visually by graphing the two inequalities on one number line.

Practice Problems ▶

Glossary

solution to an inequality

solution to an inequality

A solution to an inequality is a value of the variable that makes the inequality true. For example, $x = \text-3$ is a solution to the inequality $x < \text-1$, but $x = 3$ is not a solution.